题目内容
19．已知抛物线C：y2=4x的焦点为F，直线y=$\sqrt{3}$（x-1）与C交于A，B（A在x轴上方）两点，若$\overrightarrow{AF}$=m$\overrightarrow{FB}$，则m的值为（ ）| A． | $\sqrt{3}$ | B． | $\frac{3}{2}$ | C． | 2 | D． | 3 |
分析 由题意画出图形，联立方程组求出A，B的坐标，进一步得到|AF|，|BF|的长度，结合$\overrightarrow{AF}$=m$\overrightarrow{FB}$把m转化为线段的长度比得答案．
解答 解：如图，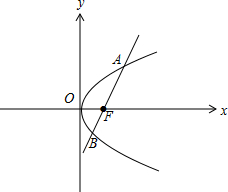
联立$\left\{\begin{array}{l}{y=\sqrt{3}（x-1）}\\{{y}^{2}=4x}\end{array}\right.$，解得${x}_{1}=3，{x}_{2}=\frac{1}{3}$，
∵A在x轴上方，∴${x}_{A}=3，{x}_{B}=\frac{1}{3}$，
则|AF|=xA+1=4，|BF|=${x}_{B}+1=\frac{1}{3}+1=\frac{4}{3}$，
由$\overrightarrow{AF}$=m$\overrightarrow{FB}$，得$m=\frac{|AF|}{|BF|}=\frac{4}{\frac{4}{3}}=3$．
故选：D．
点评 本题考查了抛物线的简单几何性质，考查了数形结合的解题思想方法，考查了数学转化思想方法，是中档题．
练习册系列答案
相关题目
11．
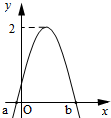如图是函数$f（x）=Asin（2x+φ）（|φ|≤\frac{π}{2}）$图象的一部分，对不同的x1，x2∈[a，b]，若 f（x1）=f（x2），有$f（{x_1}+{x_2}）=\sqrt{3}$，则（ ）
如图是函数$f（x）=Asin（2x+φ）（|φ|≤\frac{π}{2}）$图象的一部分，对不同的x1，x2∈[a，b]，若 f（x1）=f（x2），有$f（{x_1}+{x_2}）=\sqrt{3}$，则（ ）| A． | f（x）在$（-\frac{5π}{12}，\frac{π}{12}）$上是减函数 | B． | f（x）在$（\frac{π}{3}，\frac{5π}{6}）$上是减函数 | ||
| C． | f（x）在$（-\frac{5π}{12}，\frac{π}{12}）$上是增函数 | D． | f（x）在$（\frac{π}{3}，\frac{5π}{6}）$上是减函数 |
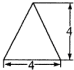一个四棱锥的底面是正方形，其正视图和侧视图均为如图所示的等腰三角形，则该四棱锥的侧面积为16$\sqrt{5}$．
7．若${∫}_{0}^{1}$（x2+mx）dx=0，则实数m的值为（ ）
| A． | -$\frac{1}{3}$ | B． | -2 | C． | -1 | D． | -$\frac{2}{3}$ |