若${∫} {0}^{1}$(x2+mx)dx=0.则实数m的值为( )A．-$\frac{1}{3}$B．-2C．-1D．-$\frac{2}{3}$ 题目和参考答案——青夏教育精英家教网—

题目内容

7．若${∫}_{0}^{1}$（x²+mx）dx=0，则实数m的值为（　　）

A．

-$\frac{1}{3}$

B．

-2

C．

-1

D．

-$\frac{2}{3}$

分析求出被积函数的原函数，然后分别代入积分上限和积分下限作差，由积分值为0求得m的值．

解答解：∵${∫}_{0}^{1}（{x}^{2}+mx）dx$=$（\frac{1}{3}{x}^{3}+\frac{1}{2}m{x}^{2}）{|}_{0}^{1}=\frac{1}{3}+\frac{1}{2}m=0$，
∴m=-$\frac{2}{3}$．
故选：D．

点评本题考查了定积分，关键是求出被积函数的原函数，是基础题．

练习册系列答案

相关题目

20．抛物线y=-4x²的准线方程为（　　）

19．求“方程${（{\frac{3}{5}}）^x}+{（{\frac{4}{5}}）^x}=1$的解”有如下解题思路：设$f（x）={（{\frac{3}{5}}）^x}+{（{\frac{4}{5}}）^x}$，则f（x）在R上单调递减，且f（2）=1，以方程有唯一解x=2．类比上述解法，方程x⁶+x²=（x+2）³+x+2的解为-1或2．

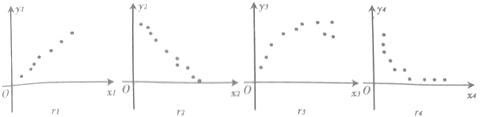
r₁＞r₃＞r₄＞r₂

r₃＞r₁＞r₂＞r₄

r₃＞r₁＞r₄＞r₂

r₁＞r₃＞r₂＞r₄

2．观察等式：$f（\frac{1}{3}）+f（\frac{2}{3}）=1，f（\frac{1}{4}）+f（\frac{2}{4}）+f（\frac{3}{4}）=\frac{3}{2}，f（\frac{1}{5}）+f（\frac{2}{5}）+f（\frac{3}{5}）+f（\frac{4}{5}）=2，f（\frac{1}{6}）+f（\frac{2}{6}）+f（\frac{3}{6}）+f（\frac{4}{6}）+f（\frac{5}{6}）=\frac{5}{2}$，…由以上几个等式的规律可猜想$f（\frac{1}{2015}）+f（\frac{2}{2015}）+f（\frac{3}{2015}）+…f（\frac{2013}{2015}）+f（\frac{2014}{2015}）$=1007．

12．在三棱锥P-ABC中，PA⊥平面ABC，AB⊥BC且PA=AB=4，BC=2，则三棱锥P-ABC的外接球的体积为（　　）

19．已知抛物线C：y²=4x的焦点为F，直线y=$\sqrt{3}$（x-1）与C交于A，B（A在x轴上方）两点，若$\overrightarrow{AF}$=m$\overrightarrow{FB}$，则m的值为（　　）

15．已知圆C：x²+y²=25和两点A（3，4），B（-1，2），则直线AB与圆C的位置关系为相交，若点P在圆C上，且S_△ABP=$\frac{5}{2}$，则满足条件的P点共有4个．

14．椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）的左右焦点为F₁、F₂，若C上存在一点P，使得|PF₁|=2|PF₂|，则C的离心率的范围是$[\frac{1}{3}，1）$．

试题分类