题目内容
6.已知F1、F2分别是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$的左、右焦点,P为双曲线右支上的任意一点且$\frac{{|P{F_1}{|^2}}}{{|P{F_2}|}}=8a$,则双曲线离心率的取值范围是( )| A. | (1,2] | B. | [2+∞) | C. | (1,3] | D. | [3,+∞) |
分析 化简$\frac{|P{F}_{1}{|}^{2}}{|P{F}_{2}|}$=$\frac{(2a+|P{F}_{2}|)^{2}}{|P{F}_{2}|}$=$\frac{4{a}^{2}}{|P{F}_{2}|}$+4a+|PF2|,利用基本不等式,再利用焦半径公式,即可求出双曲线离心率的取值范围.
解答 解:由定义知:|PF1|-|PF2|=2a,所以|PF1|=2a+|PF2|,
所以$\frac{|P{F}_{1}{|}^{2}}{|P{F}_{2}|}$=$\frac{(2a+|P{F}_{2}|)^{2}}{|P{F}_{2}|}$=$\frac{4{a}^{2}}{|P{F}_{2}|}$+4a+|PF2|≥8a,
当且仅当$\frac{4{a}^{2}}{|P{F}_{2}|}$=|PF2|,即|PF2|=2a时取得等号
设P(x0,y0) (x0≤-a)
由焦半径公式得:|PF2|=-ex0-a=2a
所以ex0=-3a
所以e=-$\frac{3a}{{x}_{0}}$≤3
又双曲线的离心率e>1
所以e∈(1,3]
故选:C.
点评 本题考查双曲线离心率的取值范围,考查基本不等式的运用,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
19.已知抛物线C:y2=4x的焦点为F,直线y=$\sqrt{3}$(x-1)与C交于A,B(A在x轴上方)两点,若$\overrightarrow{AF}$=m$\overrightarrow{FB}$,则m的值为( )
| A. | $\sqrt{3}$ | B. | $\frac{3}{2}$ | C. | 2 | D. | 3 |
1.某校甲、乙两个班级各有5名编号分别为1,2,3,4,5的学生进行投篮训练,每人投10次,投中的次数统计如下表:
(1)从统计数据看,甲、乙两个班哪个班的同学投篮水平更稳定(用数据说明)?
(2)在本次训练中,从两班中分别任选一个同学,比较两人的投中次数,求甲班同学投中次数多于乙班同学投中次数的概率.
| 学生 | 1号 | 2号 | 3号 | 4号 | 5号 |
| 甲班 | 6 | 5 | 7 | 9 | 8 |
| 乙班 | 4 | 8 | 9 | 7 | 7 |
(2)在本次训练中,从两班中分别任选一个同学,比较两人的投中次数,求甲班同学投中次数多于乙班同学投中次数的概率.
18.已知函数f(x)对任意x,满足f(x)=sinx+2f($\frac{π}{2}$-x),则f($\frac{5π}{4}$)=( )
| A. | -$\sqrt{2}$ | B. | -$\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\sqrt{2}$ |
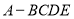 中,底面
中,底面 为矩形,侧面
为矩形,侧面 底面
底面 ,
, ,
, .
.
 ;
; 与平面
与平面 所成的角为
所成的角为 ,求二面角
,求二面角 的余弦值的大小.
的余弦值的大小. ,当
,当 时,函数
时,函数 的图象关于
的图象关于 轴对称,数列
轴对称,数列 的前
的前 项和为
项和为 ,且
,且 .
. ,求数列
,求数列 的前
的前 .
.