题目内容
若函数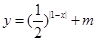
的图像与
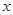轴有公共点，则
的取值范围是_______．
.
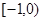解析试题分析：由题意得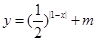：的图像与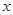轴有交点
方程
有解，∴
，
∵
，∴
，∴的取值范围是.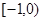
考点：1.函数零点的概念；2.指数函数的性质.
练习册系列答案
小学课堂作业系列答案
金博士一点全通系列答案
相关题目
小学课堂作业系列答案金博士一点全通系列答案题目内容
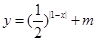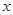若函数的图像与轴有公共点，则的取值范围是_______．
.
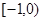解析试题分析：由题意得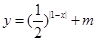：的图像与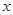轴有交点方程有解，∴，
∵，∴，∴的取值范围是.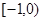
考点：1.函数零点的概念；2.指数函数的性质.
小学课堂作业系列答案金博士一点全通系列答案
的定义域为 ．
满足
，则
的值为 ．
对任意的
有
恒成立，求实数
的取值范围
.
的方程
有实根，则实数
的取值范围为________．
，方程
有五个不同的实数解时，
的取值范围为 ．
<x≤m＋
(k∈Z)对称．其中正确命题的序号是________．
)上不是凸函数的是________．