题目内容
过双曲线
-
=1(a>0,b>0)的左焦点F引圆x2+y2=a2的切线,切点为A,延长FA交双曲线右支于点P,若A为线段PF靠近F的三等分点,则该双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
分析:设出点A,和P的坐标,求出所用向量的坐标,利用
•
=0结合点A在圆上求出A的坐标,利用
=3
把P的坐标用A的坐标表示,代入双曲线方程后整理运算即可得到答案.
| OA |
| FA |
| FP |
| FA |
把P的坐标用A的坐标表示,代入双曲线方程后整理运算即可得到答案.
解答: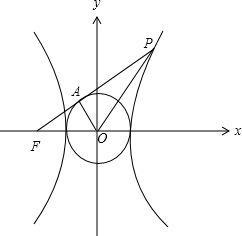 解:如图,
解:如图,
F(-c,0),设A(x0,y0),P(x1,y1).
则
=(x0,y0),
=(x0+c,y0),
=(x1+c,y1).
由
•
=0,得x02+cx0+y02=0,即cx0+a2=0.
∴x0=-
,y02=a2-x02=a2-
=
.
又A为线段PF靠近F的三等分点,
∴
=3
,∴
,即
.
代入
-
=1(a>0,b>0)得,
-
=1①
把x0,y0代入①得,
-
=1,
整理得,4c2=13a2,解得e=
.
故选D.
 解:如图,
解:如图,F(-c,0),设A(x0,y0),P(x1,y1).
则
| OA |
| FA |
| FP |
由
| OA |
| FA |
∴x0=-
| a2 |
| c |
| a4 |
| c2 |
| a2b2 |
| c2 |
又A为线段PF靠近F的三等分点,
∴
| FP |
| FA |
|
|
代入
| x2 |
| a2 |
| y2 |
| b2 |
| (3x0+2c)2 |
| a2 |
| 9y02 |
| b2 |
把x0,y0代入①得,
(2c-
| ||
| a2 |
9•
| ||
| b2 |
整理得,4c2=13a2,解得e=
| ||
| 2 |
故选D.
点评:本题考查了双曲线的简单几何性质,考查了直线与圆的位置关系,训练了利用数量积解题,考查了学生的计算能力,是中档题.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
过双曲线
-
=1的左焦点F作⊙O:x2+y2=a2的两条切线,记切点为A,B,双曲线左顶点为C,若∠ACB=120°,则双曲线的渐近线方程为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、y=±
| ||||
B、y=±
| ||||
C、y=±
| ||||
D、y=±
|