题目内容
过双曲线
-
=1的左焦点F作⊙O:x2+y2=a2的两条切线,记切点为A,B,双曲线左顶点为C,若∠ACB=120°,则双曲线的渐近线方程为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、y=±
| ||||
B、y=±
| ||||
C、y=±
| ||||
D、y=±
|
分析:根据双曲线的方程得到渐近线为y=±
x,结合题中的条件画出图象进而得到∠AFO=30°,即得到a与c的关系式,进而得到a与b的关系式,即可得到答案.
| b |
| a |
解答:解:由题意可得:双曲线的方程为
-
=1,
所以双曲线的渐近线方程为y=±
x.
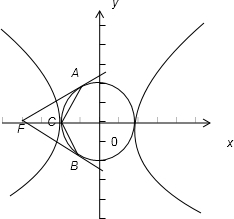
因为若∠ACB=120°,
所以根据图象的特征可得:∠AFO=30°,
所以c=2a,
又因为b2=c2-a2,
所以
=
,
所以双曲线的渐近线方程为y=±
x.
故选A.
| x2 |
| a2 |
| y2 |
| b2 |
所以双曲线的渐近线方程为y=±
| b |
| a |

因为若∠ACB=120°,
所以根据图象的特征可得:∠AFO=30°,
所以c=2a,
又因为b2=c2-a2,
所以
| b |
| a |
| 3 |
所以双曲线的渐近线方程为y=±
| 3 |
故选A.
点评:解决此类问题的关键是熟练掌握双曲线与圆的位置关系,结合有关条件得到a、b与c的关系,进而得到答案.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目