Question

过双曲线

x2

a2

-

y2

b2

=1（a＞0，b＞0）的一个焦点F引它到渐进线的垂线，垂足为M，延长FM交y轴于E，若

FM

=2

ME

，则该双曲线离心率为（　　）

• A．

  3

  2

• B．

  6

  2

• C．

  3

• D．3

Answer 1

分析：先利用FM与渐近线垂直，写出直线FM的方程，从而求得点E的坐标，利用已知向量式，求得点M的坐标，最后由点M在渐进线上，代入得a、b、c间的等式，进而变换求出离心率

解答：解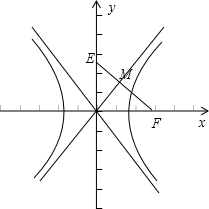：设F（c，0），则c²=a²+b²
∵双曲线

x2

a2

-

y2

b2

=1（a＞0，b＞0）的渐进线方程为y=±

b

a

x
∴垂线FM的斜率为-

a

b

∴直线FM的方程为y=-

a

b

（x-c）
令x=0，得点E的坐标（0，

ac

b

）
设M（x，y），∵

FM

=2

ME

，
∴（x-c，y）=2（-x，

ac

b

-y）
∴x-c=-2x且y=

2ac

b

-2y
即x=

c

3

，y=

2ac

3b

代入y=

b

a

x
得

2ac

3b

=

bc

3a

，即2a²=b²，
∴2a²=c²-a²，
∴

c2

a2

=3，

c

a

=

3

∴该双曲线离心率为

3

故选C

点评：本题考查了双曲线的几何性质，求双曲线离心率的方法，向量在解析几何中的应用