题目内容
【题目】对于函数![]() ,定义f1(x)=f(x),fn+1(x)=f[fn(x)](n∈N*),已知偶函数g(x)的定义域为(﹣∞,0)∪(0,+∞),g(1)=0,当x>0且x≠1时,g(x)=f2018(x).
,定义f1(x)=f(x),fn+1(x)=f[fn(x)](n∈N*),已知偶函数g(x)的定义域为(﹣∞,0)∪(0,+∞),g(1)=0,当x>0且x≠1时,g(x)=f2018(x).
(1)求f2(x),f3(x),f4(x),f2018(x);
(2)求出函数y=g(x)的解析式;
(3)若存在实数a、b(a<b),使得函数g(x)在[a,b]上的值域为[mb,ma],求实数m的取值范围.
【答案】(1)见解析; (2)g(x)=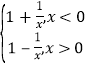 ;(3)(﹣
;(3)(﹣![]() ,0).
,0).
【解析】
(1)根据函数关系代入计算进行求解即可;(2)由偶函数的定义,计算可得所求解析式;(3)根据函数奇偶性和单调性的性质,结合函数的值域关系进行求解即可.
(1)因为函数![]()
定义f1(x)=f(x),fn+1(x)=f[fn(x)](n∈N*),f1(x)=![]() ,
,
f2(x)=f[f1(x)]= ![]() =
=![]() ,(x≠0且x≠1),
,(x≠0且x≠1),
f3(x)=f[f2(x)]= ![]() =x,(x≠0且x≠1),
=x,(x≠0且x≠1),
f4(x)=f[f3(x)]= ![]() ,(x≠0且x≠1),
,(x≠0且x≠1),
故对任意的n∈N,有f3n+i(x)=fi(x)(i=2,3,4),
于是f2018(x)=f3×672+2=f2(x)=1﹣![]() ,(x≠0且x≠1);
,(x≠0且x≠1);
(2)当x>0且x≠1时,g(x)=f2018(x)=1﹣![]() ,
,
又g(1)=0,
由g(x)为偶函数,当x<0时,﹣x>0,g(x)=g(﹣x)=1+![]() ,
,
可得g(x)=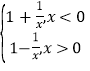 ;
;
(3)由于y=g(x)的定义域为(﹣∞,0)∪(0,+∞),
又a<b,mb<ma,可知a与b同号,且m<0,
进而g(x)在[a,b]递减,且a<b<0,
当a,b∈(0,1)时,g(x)=1﹣![]() 为增函数,
为增函数,
故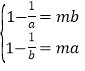 ,即m=
,即m=![]() =
=![]() ,
,
得a﹣1=b﹣1,即a=b,与a<b矛盾,∴此时a,b不存在;
函数y=g(x)的图象,如图所示.由题意,有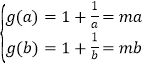 ,
,
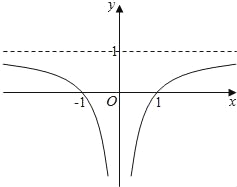
故a,b是方程1+![]() =mx的两个不相等的负实数根,
=mx的两个不相等的负实数根,
即方程mx2﹣x﹣1=0在(﹣∞,0)上有两个不相等的实根,
于是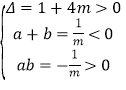 ,解得﹣
,解得﹣![]() <m<0.
<m<0.
综合上述,得实数m的取值范围为(﹣![]() ,0).
,0).

 阅读快车系列答案
阅读快车系列答案