题目内容
6. 在棱长为1的正方体ABCD-A1B1C1D1中,给出以下命题:
在棱长为1的正方体ABCD-A1B1C1D1中,给出以下命题:①直线A1B与B1C所成的角为60°;
②动点M在表面上从点A到点C1经过的最短路程为1+$\sqrt{2}$;
③若N是线段AC1上的动点,则直线CN与平面BDC1所成角的正弦值的取值范围是[$\frac{\sqrt{3}}{3}$,1];
④若P、Q是线段AC上的动点,且PQ=1,则四面体PQB1D1的体积恒为$\frac{\sqrt{2}}{6}$.
则上述命题中正确的有①③④.(填写所有正确命题的序号)
分析 ①先证明A1B与A1D所成角为60°,又B1C∥A1D,可得直线A1B与B1C所成的角为60°,判断①正确;
②将面AB1与面A1C1展开,那么动点M在表面上从点A到点C1经过的最短路程为$\sqrt{5}$判断②错误;
③由平面BDC1⊥平面ACC1,结合线面角的定义分别求出直线CN与平面BDC1所成角的正弦值最大值与最小值判断③正确;
④在PQ变化过程中,四面体PQB1D1的顶点D1到底面B1PQ的距离不变,底面积不变,则体积不变,求出体积判断④正确.
解答 解:①在△A1BD中,每条边都是$\sqrt{2}$,即为等边三角形,∴A1B与A1D所成角为60°,
又B1C∥A1D,∴直线A1B与B1C所成的角为60°,正确;
②将面AB1与面A1C1展开,那么动点M在表面上从点A到点C1经过的最短路程为AC1,AC1=$\sqrt{5}$,错误;
③如图,由正方体可得平面BDC1⊥平面ACC1,当N点位于AC1上,且使CN⊥平面BDC1时,直线CN与平面BDC1所成角的正弦值最大为1,
当N与C1重合时,连接CN交平面BDC1所得斜线最长,直线CN与平面BDC1所成角的正弦值最小等于$\frac{\sqrt{3}}{3}$,
∴直线CN与平面BDC1所成角的正弦值的取值范围是[$\frac{\sqrt{3}}{3}$,1],正确;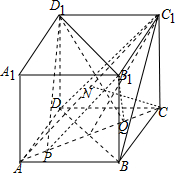
④连接B1P,B1Q,设D1到平面B1AC的距离为h,则h=$\frac{2\sqrt{3}}{3}$,B1到直线AC的距离为$\frac{\sqrt{6}}{2}$,
则四面体PQB1D1的体积V=$\frac{1}{3}×\frac{1}{2}×1×\frac{\sqrt{6}}{2}×\frac{2}{3}\sqrt{3}=\frac{\sqrt{2}}{6}$,正确.
∴正确的命题是①③④.
故答案为:①③④
点评 本题考查了命题的真假判断与应用,考查了空间点线面的位置关系,考查了空间想象能力和思维能力,是中档题.

 如图,在底面是矩形的四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB=2,BC=4,E是PD的中点,
如图,在底面是矩形的四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB=2,BC=4,E是PD的中点, 某人在5场投篮比赛中得分的茎叶图如图所示,若5场比赛的平均得分为11分,则则5场比赛得分的方差为$\frac{34}{5}$.
某人在5场投篮比赛中得分的茎叶图如图所示,若5场比赛的平均得分为11分,则则5场比赛得分的方差为$\frac{34}{5}$.