题目内容
【题目】已知数列![]() 是首项为1的等差数列,数列
是首项为1的等差数列,数列![]() 满足
满足![]() ,且
,且![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)令![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() .
.
【答案】(1) ![]() ;(2)
;(2) ![]() .
.
【解析】试题分析: (1)根据数列![]() 的递推关系式以及等比数列的定义,得出
的递推关系式以及等比数列的定义,得出![]() 是一个等比数列,根据基本量运算求解即可;(2)先求出等差数列
是一个等比数列,根据基本量运算求解即可;(2)先求出等差数列![]() 的通项公式,代入
的通项公式,代入![]() ,根据错位相减法求出数列的前n项和.
,根据错位相减法求出数列的前n项和.
试题解析:
(1)∵![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∴![]() 是首项为
是首项为![]() ,公比为3的等比数列,
,公比为3的等比数列,
∴![]() ,即
,即![]() .
.
(2)由(1)知, ![]() ,∴
,∴![]() ,则
,则![]() ,
,
∴![]() ,
,
令![]() ,①
,①
![]() ,②
,②
①![]() ②得
②得![]()
∴![]() .∴
.∴![]() .
.
点睛: 用错位相减法求和应注意的问题 :(1)要善于识别题目类型,特别是等比数列公比为负数的情形; (2)在写出“Sn”与“qSn”的表达式时应特别注意将两式“错项对齐”以便下一步准确写出“Sn-qSn”的表达式; (3)在应用错位相减法求和时,若等比数列的公比为参数,应分公比等于1和不等于1两种情况求解.

 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案【题目】《中国好声音(![]()
![]()
![]()
![]() )》是由浙江卫视联合星空传媒旗下灿星制作强力打造的大型励志专业音乐评论节目,于2012年7月13日在浙江卫视播出.每期节目有四位导师参加.导师背对歌手,当每位参赛选手演唱完之前有导师为其转身,则该选手可以选择加入为其转身的导师的团队中接受指导训练.已知某期《中国好声音》中,6位选手唱完后,四位导师为其转身的情况如下表所示:
)》是由浙江卫视联合星空传媒旗下灿星制作强力打造的大型励志专业音乐评论节目,于2012年7月13日在浙江卫视播出.每期节目有四位导师参加.导师背对歌手,当每位参赛选手演唱完之前有导师为其转身,则该选手可以选择加入为其转身的导师的团队中接受指导训练.已知某期《中国好声音》中,6位选手唱完后,四位导师为其转身的情况如下表所示:
导师转身人数(人) | 4 | 3 | 2 | 1 |
获得相应导师转身的选手人数(人) | 1 | 2 | 2 | 1 |
现从这6位选手中随机抽取两人考查他们演唱完后导师的转身情况.
(1)求选出的两人导师为其转身的人数和为4的概率;
(2)记选出的2人导师为其转身的人数之和为![]() ,求
,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
【题目】随着科学技术的飞速发展,手机的功能逐渐强大,很大程度上代替了电脑、电视.为了了解某高校学生平均每天使用手机的时间是否与性别有关,某调查小组随机抽取了![]() 名男生、
名男生、![]() 名女生进行为期一周的跟踪调查,调查结果如表所示:
名女生进行为期一周的跟踪调查,调查结果如表所示:
平均每天使用手机超过 | 平均每天使用手机不超过 | 合计 | |
男生 |
|
|
|
女生 |
|
|
|
合计 |
|
|
|
(1)能否在犯错误的概率不超过![]() 的前提下认为学生使用手机的时间长短与性别有关?
的前提下认为学生使用手机的时间长短与性别有关?
(2)在这![]() 名女生中,调查小组发现共有
名女生中,调查小组发现共有![]() 人使用国产手机,在这
人使用国产手机,在这![]() 人中,平均每天使用手机不超过
人中,平均每天使用手机不超过![]() 小时的共有
小时的共有![]() 人.从平均每天使用手机超过
人.从平均每天使用手机超过![]() 小时的女生中任意选取
小时的女生中任意选取![]() 人,求这
人,求这![]() 人中使用非国产手机的人数
人中使用非国产手机的人数![]() 的分布列和数学期望.
的分布列和数学期望.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
参考公式: 
![]()
【题目】某公司为了解用户对其产品的满意度,从A、B两地区分别随机调查了20个用户,得到用户对产品的满意度评分如下:
A地区: | 62 | 73 | 81 | 92 | 95 | 85 | 74 | 64 | 53 | 76 |
78 | 86 | 95 | 66 | 97 | 78 | 88 | 82 | 76 | 89 | |
B地区: | 73 | 83 | 62 | 51 | 91 | 46 | 53 | 73 | 64 | 82 |
93 | 48 | 95 | 81 | 74 | 56 | 54 | 76 | 65 | 79 |
(Ⅰ)根据两组数据完成两地区用户满意度评分的茎叶图,并通过茎叶图比较两地区满意度的平均值及分散程度(不要求算出具体值,给出结论即可):
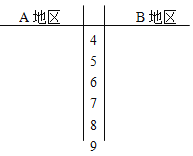
(Ⅱ)根据用户满意度评分,将用户的满意度从低到高分为三个等级:
满意度评分 | 低于70分 | 70分到89分 | 不低于90分 |
满意度等级 | 不满意 | 满意 | 非常满意 |
记事件C:“A地区用户的满意度等级高于B地区用户的满意度等级”,假设两地区用户的评价结果相互独立,根据所给数据,以事件发生的频率作为相应事件发生的概率,求C的概率。
