Question

【题目】对于函数（为自然对数的底数，），函数，给出下列结论：

①函数的图象在处的切线在轴的截距为

②函数是奇函数，且在上单调递增；

③函数存在唯一的极小值点，其中，且；

④函数存在两个极小值点，和两个极大值点，且.

其中所有正确结论的序号是（ ）

A.①②③B.①④C.①③④D.②④

Answer 1

【答案】C

【解析】

求出，写出切线点斜式方程，化简可判断①；由的定义域，即可判断②；构造函数，通过判断的单调性，得到的解，即可判断③；求出，进而求出的单调区间，极值点，根据对称性即可判断④.

对于①，，

函数的图象在处的切线方程为，

令，即所求的切线在轴上的截距为，

所以①正确；

对于②，，

定义域不关于原点对称，所以不是奇函数，所以②不正确；

对于③，，当，

当，设，

时，为增函数，

又恒成立，

在上单调递增，

即在上单调递增，

，

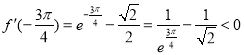，所以存在唯一的，

使得，当，

所以时，取得极小值，所以③正确；

对于④，，

显然不是极值点，取的定义域为，

此时为奇函数，

为偶函数，

，令，

转化为求与在的交点，

画出两函数图象，如下图所示，

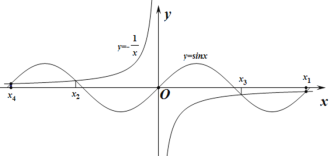
与在为奇函数，

两函数图象有四个交点，与均关于原点对称，

当时，，

，

所以时，取得极大值，时，取得极小值，

当时，时偶函数，，

，

所以时，取得极大值，时，取得极小值，

此时，所以④正确.

故选：C.