Question

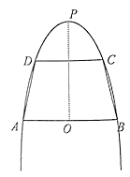
【题目】某新建小区规划利用一块空地进行配套绿化.已知空地的一边是直路，余下的外围是抛物线的一段弧，直路的中垂线恰是该抛物线的对称轴（如图），点O是的中点.拟在这个地上划出一个等腰梯形区域种植草坪，其中均在该抛物线上.经测量，直路长为60米，抛物线的顶点P到直路的距离为60米.设点C到抛物线的对称轴的距离为m米，到直路的距离为n米.

（1）求出n关于m的函数关系式.

（2）当m为多大时，等腰梯形草坪的面积最大？并求出其最大值.

Answer 1

【答案】（1）；（2），平方米

【解析】

（1）以路所在的直线为x轴，抛物线的对称轴为y轴建立平面直角坐标系，求出抛物线方程即得；

（2）由点坐标，求出，把表示为的函数，再由导数知识求得最大值．

解：（1）以路所在的直线为x轴，抛物线的对称轴为y轴建立平面直角坐标系，

则，，，

因为曲线段为抛物线的一段弧，

所以可以设抛物线的解析式为，

将点代入得：，解得，

所以抛物线的解析式为，

因为点C在抛物线上，所以

（2）设等腰梯形的面积为S，

则，

，

，

令，得或（舍去）

		10
	+	0	-
	增	极大值	减

当时，

答：当时，等腰梯形的面积最大，最大值为平方米.