题目内容
【题目】如图，在四棱锥A﹣BCDE中，底面BCDE为矩形，侧面ABC⊥底面BCDE，BC=2，CD= 
，AB=AC． 
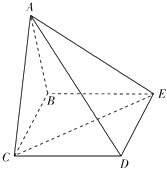
（1）证明：AD⊥CE；
（2）设CE与平面ABE所成的角为45°，求二面角C﹣AD﹣E的余弦值．
【答案】
（1）证明：取BC中点F，连接DF交CE于点O，
∵AB=AC，∴AF⊥BC．
又面ABC⊥面BCDE，∴AF⊥面BCDE，∴AF⊥CE．
再根据 
，可得∠CED=∠FDC．
又∠CDE=90°，∴∠OED+∠ODE=90°，
∴∠DOE=90°，即CE⊥DF，∴CE⊥面ADF，∴CE⊥AD．
（2）解：在面ACD内过C点作AD的垂线，垂足为G．
∵CG⊥AD，CE⊥AD，∴AD⊥面CEG，∴EG⊥AD，
则∠CGE即为所求二面角的平面角．
作CH⊥AB，H为垂足．
∵平面ABC⊥平面BCDE，矩形BCDE中，BE⊥BC，故BE⊥平面ABC，CH平面ABC，
故BE⊥CH，而AB∩BE=B，故CH⊥平面ABE，
∴∠CEH=45°为CE与平面ABE所成的角．
∵CE= 
，∴CH=EH= 
．
直角三角形CBH中，利用勾股定理求得BH= 
= 
=1，∴AH=AB﹣BH=AC﹣1；
直角三角形ACH中，由勾股定理求得AC2=CH2+AH2=3+（AC﹣1）2，∴AB=AC=2．
由面ABC⊥面BCDE，矩形BCDE中CD⊥CB，可得CD⊥面ABC，
故△ACD为直角三角形，AD= 
= 
= ，
故CG= 
= 
= 
，DG= 
= 
，
，又 
，
则 
．
【解析】（1）取BC中点F，证明CE⊥面ADF，通过证明线面垂直来达到证明线线垂直的目的．（2）在面AED内过点E作AD的垂线，垂足为G，由（1）知，CE⊥AD，则∠CGE即为所求二面角的平面角，根据三角形的边角关系进行求即可即可．
【考点精析】认真审题，首先需要了解空间中直线与直线之间的位置关系(相交直线：同一平面内，有且只有一个公共点；平行直线：同一平面内，没有公共点；异面直线： 不同在任何一个平面内，没有公共点)．
