Question

已知f（x）是定义域为R的奇函数，f（-4）=-2，f（x）的导函数f′（x）的图象如图所示，若两正数a，b满足f（a+2b）＜2，则

a+4

b+4

的取值范围是（　　）

• A．(

  1

  2

  ，

  3

  2

  )
• B．(

  1

  2

  ，

  2

  3

  )
• C．(

  2

  3

  ，2)
• D．(-2，-

  2

  3

  )

Answer 1

分析：由f（x）为奇函数及f（-4）=-2可求得f（4），根据导函数图象可判断f（x）的单调性，从而f（a+2b）＜2可化为a，b的不等式，画出点（b，a）对应的区域，

a+4

b+4

可看作（b，a）与（-4，-4）连线的斜率，由图象可求得斜率范围．

解答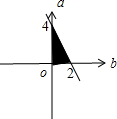：解：∵f（-4）=-2，且f（x）是定义域为R的奇函数，
∴f（4）=-f（-4）=2，
则f（a+2b）＜2，可化为f（a+2b）＜f（4），
由导函数f′（x）的图象可知，f′（x）≥0，
∴f（x）在R上单调递增，
则有a+2b＜4，
又a＞0，b＞0，
则点（b，a）对应的区域如图所示：

a+4

b+4

可看作（b，a）与（-4，-4）连线的斜率，设为k，
由图象可知

0-(-4)

2-(-4)

＜k＜

4-(-4)

0-(-4)

，即

2

3

＜k＜2，
∴

2

3

＜

a+4

b+4

＜2，
故选C．

点评：本题考查导数与函数单调性间的关系、斜率的计算公式，考查转化思想．