题目内容
已知以点P为圆心的圆过点A(-1,0)和B(3,4),AB的垂直平分线交圆P于点C、D,且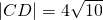 .
.
(1)求圆P的方程;
(2)设点Q在圆P上,试探究使△QAB的面积为8的点Q共有几个?并说明理由.
解:(1)因为kAB=1,AB的中点坐标为(1,2),所以直线CD的方程为y-2=-(x-1),
即x+y-3=0.(3分)
设圆心P(a,b),则由P在CD上得a+b-3=0.①
又直径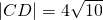 ,所以
,所以 ,所以(a+1)2+b2=40.②
,所以(a+1)2+b2=40.②
①代入②消去a得-4b-12=0,解得b=6或b=-2.
当b=6时,a=-3;当b=-2时,a=5,所以圆心P(-3,6)或P(5,-2),所以圆P的方程为(x+3)2+(y-6)2=40或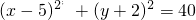 .(8分)
.(8分)
(2)因为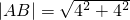 =
= ,所以当△QAB面积为8时,点Q到直线AB的距离为
,所以当△QAB面积为8时,点Q到直线AB的距离为 .(10分)
.(10分)
又圆心到直线AB的距离为 ,圆P的半径
,圆P的半径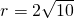 ,且
,且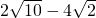
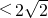 ,
,
所以圆上共有两个点Q,使△QAB的面积为8.(15分)
分析:(1)因为kAB=1,AB的中点坐标为(1,2),所以直线CD的方程为y-2=-(x-1),设圆心P(a,b),则由P在CD上得a+b-3=0,由此能求出圆P的方程.
(2)因为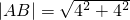 =
= ,所以当△QAB面积为8时,点Q到直线AB的距离为
,所以当△QAB面积为8时,点Q到直线AB的距离为 .又圆心到直线AB的距离为
.又圆心到直线AB的距离为 ,圆P的半径
,圆P的半径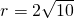 ,且
,且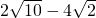
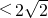 ,由此知圆上共有两个点Q,使△QAB的面积为8.
,由此知圆上共有两个点Q,使△QAB的面积为8.
点评:本题考查直线和圆的性质和应用,解题时要注意直线和圆的位置关系的合理运用.
即x+y-3=0.(3分)
设圆心P(a,b),则由P在CD上得a+b-3=0.①
又直径
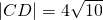 ,所以
,所以 ,所以(a+1)2+b2=40.②
,所以(a+1)2+b2=40.②①代入②消去a得-4b-12=0,解得b=6或b=-2.
当b=6时,a=-3;当b=-2时,a=5,所以圆心P(-3,6)或P(5,-2),所以圆P的方程为(x+3)2+(y-6)2=40或
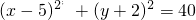 .(8分)
.(8分)(2)因为
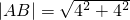 =
= ,所以当△QAB面积为8时,点Q到直线AB的距离为
,所以当△QAB面积为8时,点Q到直线AB的距离为 .(10分)
.(10分)又圆心到直线AB的距离为
 ,圆P的半径
,圆P的半径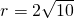 ,且
,且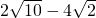
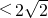 ,
,所以圆上共有两个点Q,使△QAB的面积为8.(15分)
分析:(1)因为kAB=1,AB的中点坐标为(1,2),所以直线CD的方程为y-2=-(x-1),设圆心P(a,b),则由P在CD上得a+b-3=0,由此能求出圆P的方程.
(2)因为
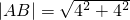 =
= ,所以当△QAB面积为8时,点Q到直线AB的距离为
,所以当△QAB面积为8时,点Q到直线AB的距离为 .又圆心到直线AB的距离为
.又圆心到直线AB的距离为 ,圆P的半径
,圆P的半径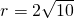 ,且
,且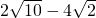
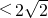 ,由此知圆上共有两个点Q,使△QAB的面积为8.
,由此知圆上共有两个点Q,使△QAB的面积为8.点评:本题考查直线和圆的性质和应用,解题时要注意直线和圆的位置关系的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目