题目内容
已知以点P为圆心的圆经过点A(-1,0)和B(3,4),线段AB的垂直平分线交圆P于点C和D,且|CD|=4| 10 |
(1)求直线CD的方程;
(2)求圆P的方程.
分析:(1)直接用点斜式求出直线CD的方程;
(2)根据条件得知|PA|为圆的半径,点P在直线CD上,列方程求得圆心P坐标,从而求出圆P的方程.
(2)根据条件得知|PA|为圆的半径,点P在直线CD上,列方程求得圆心P坐标,从而求出圆P的方程.
解答:解:(1)直线AB的斜率k=1,AB中点坐标为(1,2),…(3分)
∴直线CD方程为y-2=-(x-1)即x+y-3=0 …(6分)
(2)设圆心P(a,b),则由点P在直线CD上得:
a+b-3=0 ①…(8分)
又直径|CD|=4
,∴|PA|=2
∴(a+1)2+b2=40 ②…(10分)
由①②解得
或
∴圆心P(-3,6)或P(5,-2)…(12分)
∴圆P的方程为(x+3)2+(y-6)2=40 或(x-5)2+(y+2)2=40…(14分)
∴直线CD方程为y-2=-(x-1)即x+y-3=0 …(6分)
(2)设圆心P(a,b),则由点P在直线CD上得:
a+b-3=0 ①…(8分)
又直径|CD|=4
| 10 |
| 10 |
∴(a+1)2+b2=40 ②…(10分)
由①②解得
|
|
∴圆心P(-3,6)或P(5,-2)…(12分)
∴圆P的方程为(x+3)2+(y-6)2=40 或(x-5)2+(y+2)2=40…(14分)
点评:此题考查直线方程的点斜式,和圆的标准方程.

练习册系列答案
相关题目
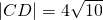 .
.