题目内容
已知在数列{an}中,a1=t,a2=t2(t>0且t≠1).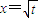 是函数f(x)=an-1x3-3[(t+1)an-an+1]x+1(n≥2)的一个极值点.
是函数f(x)=an-1x3-3[(t+1)an-an+1]x+1(n≥2)的一个极值点.(1)证明数列{an+1-an}是等比数列,并求数列{an}的通项公式;
(2)记
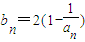 ,当t=2时,数列{bn}的前n项和为Sn,求使Sn>2008的n的最小值;
,当t=2时,数列{bn}的前n项和为Sn,求使Sn>2008的n的最小值;(3)当t=2时,是否存在指数函数g(x),使得对于任意的正整数n有
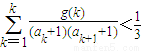 成立?若存在,求出满足条件的一个g(x);若不存在,请说明理由.
成立?若存在,求出满足条件的一个g(x);若不存在,请说明理由.
【答案】分析:(1)由函数求导令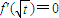 ,即
,即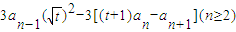 .变形可得an+1-an=t(an-an-1)符合等比数列的定义,利用通项公式求解.
.变形可得an+1-an=t(an-an-1)符合等比数列的定义,利用通项公式求解.
(2)由(1)求得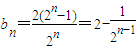 ,再求得Sn=
,再求得Sn=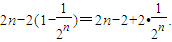 由Sn>2008,得
由Sn>2008,得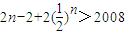 ,
,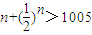 ,当n≤1400时,
,当n≤1400时,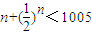 ,当n≥1005时,
,当n≥1005时,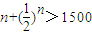 ,取得n最小值
,取得n最小值
(3)由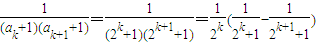 想到裂项相消法求和,由其结构不妨设g(k)=2k,运算验证即可.
想到裂项相消法求和,由其结构不妨设g(k)=2k,运算验证即可.
解答:解:(1)f'(x)=3an-1x2-3[(t+1)an-an+1](n≥2).
由题意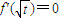 ,即
,即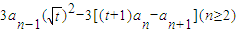 .(1分)
.(1分)
∴an+1-an=t(an-an-1)(n≥2)
∵t>0且t≠1,∴数列{an+1-an}是以t2-t为首项,t为公比的等比数列,(2分)
∴an+1-an=(t2-t)tn-1=(t-1)•tn,
∴a2-a1=(t-1)t,
a3-a2=(t-1)•t2,
an-an-1=(t-1)tn-1
以上各式两边分别相加得an-a1=(t-1)(t+t2+tn-1),∴an=tn(n≥2),
当n=1时,上式也成立,∴an=tn(5分)
(2)当t=2时,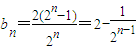
∴
=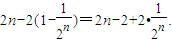 (7分)
(7分)
由Sn>2008,得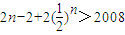 ,
,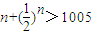 ,(8分)
,(8分)
当 ,
,
因此n的最小值为1005.(10分)
(3)∵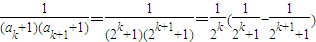
令g(k)=2k,则有: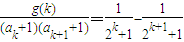
则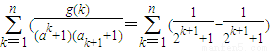 =
=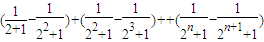 =
=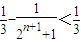 (13分)
(13分)
即函数g(k)=2x满足条件.
点评:本题主要考查函数求导,变形求数列的通项公式和前n项和以及数列不等式的解法,多数是用放缩法.
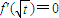 ,即
,即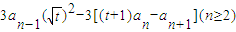 .变形可得an+1-an=t(an-an-1)符合等比数列的定义,利用通项公式求解.
.变形可得an+1-an=t(an-an-1)符合等比数列的定义,利用通项公式求解.(2)由(1)求得
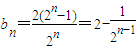 ,再求得Sn=
,再求得Sn=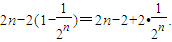 由Sn>2008,得
由Sn>2008,得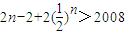 ,
,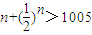 ,当n≤1400时,
,当n≤1400时,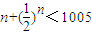 ,当n≥1005时,
,当n≥1005时,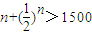 ,取得n最小值
,取得n最小值(3)由
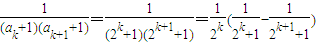 想到裂项相消法求和,由其结构不妨设g(k)=2k,运算验证即可.
想到裂项相消法求和,由其结构不妨设g(k)=2k,运算验证即可.解答:解:(1)f'(x)=3an-1x2-3[(t+1)an-an+1](n≥2).
由题意
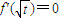 ,即
,即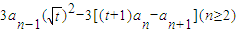 .(1分)
.(1分)∴an+1-an=t(an-an-1)(n≥2)
∵t>0且t≠1,∴数列{an+1-an}是以t2-t为首项,t为公比的等比数列,(2分)
∴an+1-an=(t2-t)tn-1=(t-1)•tn,
∴a2-a1=(t-1)t,
a3-a2=(t-1)•t2,
an-an-1=(t-1)tn-1
以上各式两边分别相加得an-a1=(t-1)(t+t2+tn-1),∴an=tn(n≥2),
当n=1时,上式也成立,∴an=tn(5分)
(2)当t=2时,
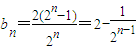
∴

=
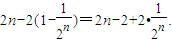 (7分)
(7分)由Sn>2008,得
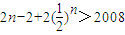 ,
,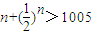 ,(8分)
,(8分)当
 ,
,因此n的最小值为1005.(10分)
(3)∵
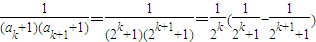
令g(k)=2k,则有:
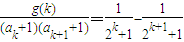
则
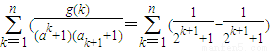 =
=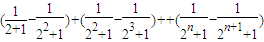 =
=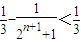 (13分)
(13分)即函数g(k)=2x满足条件.
点评:本题主要考查函数求导,变形求数列的通项公式和前n项和以及数列不等式的解法,多数是用放缩法.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目