题目内容
设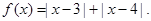
(Ⅰ)求函数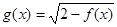 的定义域;
的定义域;
(Ⅱ)若存在实数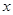 满足
满足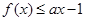 ,试求实数
,试求实数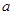 的取值范围.
的取值范围.
(Ⅰ)[ ,
, ],(Ⅱ)(-∞,-2)∪[
],(Ⅱ)(-∞,-2)∪[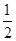 ,+∞).
,+∞).
解析试题分析:先将绝对值函数去绝对值,再求定义域,利用图像解不等式.
试题解析:(Ⅰ)f(x)=|x-3|+|x-4|= 2分
2分
作函数y=f(x)的图象,它与直线y=2交点的横坐标为 和
和 ,由图象知
,由图象知
不等式 的定义域为[
的定义域为[ ,
, ]. 5分
]. 5分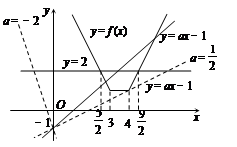

(Ⅱ)函数y=ax-1的图象是过点(0,-1)的直线.
当且仅当函数y=f(x)与直线y=ax-1有公共点时,存在题设的x.
由图象知,a取值范围为(-∞,-2)∪[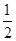 ,+∞). 10分
,+∞). 10分
考点:含绝对值式,求定义域,图像法解不等式.

练习册系列答案
相关题目
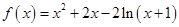 .
. 的单调区间;
的单调区间; 时,是否存在整数
时,是否存在整数 ,使不等式
,使不等式 恒成立?若存在,求整数
恒成立?若存在,求整数 的方程
的方程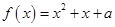 在
在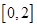 上恰有两个相异实根,求实数
上恰有两个相异实根,求实数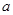 的取值范围.
的取值范围.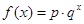 ;②
;②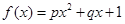 ;③
;③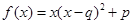 .(以上三式中
.(以上三式中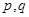 均为常数,且
均为常数,且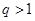 )
)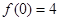 ,
,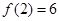 ,求出所选函数
,求出所选函数 的解析式(注:函数定义域是
的解析式(注:函数定义域是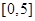 .其中
.其中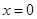 表示8月1日,
表示8月1日,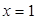 表示9月1日,…,以此类推);
表示9月1日,…,以此类推); 千件,需另投入成本为
千件,需另投入成本为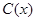 ,当年产量不足80千件时,
,当年产量不足80千件时, (万元).当年产量不小于80千件时,
(万元).当年产量不小于80千件时, (万元).每件商品售价为0.05万元.通过市场分析,该厂生产的商品能全部售完.
(万元).每件商品售价为0.05万元.通过市场分析,该厂生产的商品能全部售完. (万元)关于年产量
(万元)关于年产量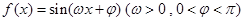 在一个周期内的部分对应值如下表:
在一个周期内的部分对应值如下表:
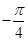

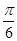

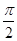
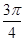


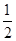
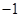
 的解析式;
的解析式;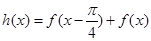 ,
,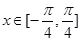 ,求
,求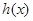 的最大值和最小值.
的最大值和最小值. 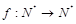 使得对于所有
使得对于所有 ,
, 都能被
都能被 整除.
整除.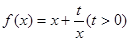 和点
和点 ,过点
,过点 作曲线
作曲线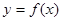 的两条切线
的两条切线 、
、 ,切点分别为
,切点分别为 、
、 .
.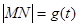 ,试求函数
,试求函数 的表达式;
的表达式; ,使得
,使得 三点共线.若存在,求出
三点共线.若存在,求出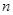 ,在区间
,在区间 内总存在
内总存在 个实数
个实数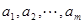 ,
, ,使得不等式
,使得不等式 成立,求
成立,求 的最大值.
的最大值. 人,(
人,( ,且
,且 为偶数),每人每年可创利
为偶数),每人每年可创利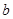 万元。据评估,在经营条件不变的前提下,每裁员1人,则留岗职员每人每年可多创利
万元。据评估,在经营条件不变的前提下,每裁员1人,则留岗职员每人每年可多创利 万元,但公司需支付下岗职员每人每年
万元,但公司需支付下岗职员每人每年 万元的生活费,并且该公司正常运转所需人数不得小于现有员工的
万元的生活费,并且该公司正常运转所需人数不得小于现有员工的 ,为获得最大的经济效益,该公司应裁员多少人?
,为获得最大的经济效益,该公司应裁员多少人? ;
; 且
且 ,求
,求 的值.
的值.