题目内容
已知直线 1:x+
1:x+ y+6=0和
y+6=0和 2:(
2:( -2)x+3y+2
-2)x+3y+2 =0,则
=0,则 1∥
1∥ 2的充要条件是
2的充要条件是 =________.
=________.
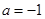
解析试题分析:首先由两直线平行可得1×3=a×(a-2),解可得a=-1或3,分别验证可得a=-1时,则l1∥l2,即可得l1∥l2⇒a=-1;反之将a=-1代入直线的方程,可得l1∥l2,即有a=-1⇒l1∥l2;综合可得l1∥l2?a=-1,即可得答案.解:根据题意,若l1∥l2,则有1×3=a×(a-2),解可得a=-1或3,反之可得,当a=-1时,直线l1:x-y+6=0,其斜率为1,直线l2:-3x+3y-2=0,其斜率为1,且l1与l2不重合,则l1∥l2,当a=3时,,直线l1:x+3y+6=0,直线l2:x+3y+6=0,l1与l2重合,此时l1与l2不平行, l1∥l2⇒a=-1,反之,a=-1⇒l1∥l2,故l1∥l2?a=-1,故a=-1
考点:直线平行的判定方法
点评:本题考查直线平行的判定方法,利用解析几何的方法判断时,要注意验证两直线是否重合

练习册系列答案
相关题目
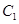 :
: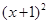 +
+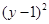 =1,圆
=1,圆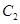 与圆
与圆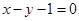 对称,则圆
对称,则圆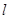 与曲线
与曲线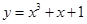 有三个不同的交点
有三个不同的交点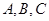 ,且
,且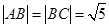 ,则直线
,则直线 ,将直线
,将直线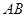 绕点
绕点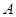 逆时针旋转
逆时针旋转 得到直线
得到直线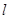 ,则直线
,则直线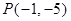 的倾斜角为
的倾斜角为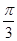 的直线
的直线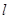 与圆
与圆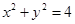 交于
交于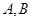 两点,则
两点,则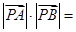 .
.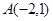 且在两坐标轴上截距相等的直线
且在两坐标轴上截距相等的直线 的方程为
的方程为 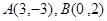 则直线
则直线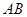 的方程是_____________
的方程是_____________