题目内容
在△ABC中,B(10,0),直线BC与圆Γ:x2+(y-5)2=25相切,切点为线段BC的中点.若△ABC的重心恰好为圆Γ的圆心,则点A的坐标为 .
(0,15) 或 (-8,-1)
解析试题分析:设BC的中点为D,设点A(x1,y1 )、C(x2,y2),则由题意可得ΓD⊥BC,且D点坐标为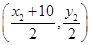 ,因为D为切点,所以圆心Γ(0,5)到直线AB的距离ΓD=r=5.设BC的方程为
,因为D为切点,所以圆心Γ(0,5)到直线AB的距离ΓD=r=5.设BC的方程为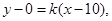 即
即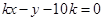 .根据点到直线的距离公式有
.根据点到直线的距离公式有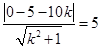 ,解得
,解得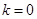 或
或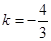 .当
.当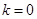 时,有
时,有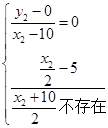 ,解得
,解得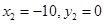 ,当
,当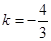 时,有
时,有 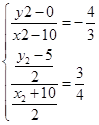 ,解得
,解得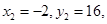 再由三角形的重心公式可以求得
再由三角形的重心公式可以求得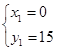 ,或
,或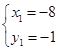 ,所以点A的坐标为(0,15)或(-8,-1).
,所以点A的坐标为(0,15)或(-8,-1).
考点:本小题主要考查直线与圆的位置关系、点到直线的距离公式、三角形的重心公式等.
点评:直线与圆相切,圆心到直线的距离等于圆半径,这个性质经常用到;另外,此类题目一般运算量较大,要仔细运算,不要漏解.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
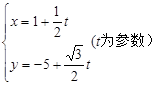 ,另一条直线的方程是
,另一条直线的方程是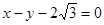 ,则两直线的交点与点
,则两直线的交点与点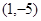 间的距离是 .
间的距离是 . 1:x+
1:x+ y+6=0和
y+6=0和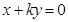 ,
,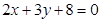 和
和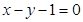 交于一点,则
交于一点,则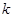 的值为 .
的值为 .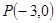 且倾斜角为
且倾斜角为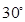 的直线和曲线
的直线和曲线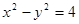 相交于A,B两点,则线段AB的长度为
相交于A,B两点,则线段AB的长度为 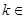 R,直线
R,直线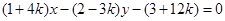 恒过一定点P,若直线
恒过一定点P,若直线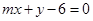 也过点P,则m = .
也过点P,则m = . 上,且A,B两点横坐标之差为
上,且A,B两点横坐标之差为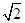 ,则A,B之间的距离为
,则A,B之间的距离为