题目内容
如图,已知正方体ABCD-A1B1C1D1的棱长为2,点E是正方形BCC1B1的中心,点F,G分别是棱C1D1,AA1的中点.设点E1,G1分别是点E,G在平面DCC1D1内的射影.
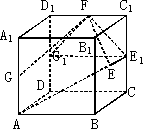
(1)求以E为顶点,以四边形FGAE在平面DCC1D1内的射影为底面的棱锥的体积;
(2)求证:直线FG1⊥平面FEE1;
(3)求异面直线E1G1与EA所成的角的正弦值.
答案:
解析:
解析:
|
(1)解:根据题意可知,所求体积即为四棱锥E-FG1DE1的体积.因为点E1,G1分别为棱CC1,DD1的中点,所以 (2)证明:在正方形DCC1D1中,FG1=FE1= (3)解:因为E1G1∥CD,AB∥CD,所以E1G1∥AB,所以∠EAB即为异面直线E1G1与EA所成的角.因为AB⊥平面BCC1B1,BE |

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
 8、如图,已知正方体ABCD-A1B1C1D1的棱长为3,点E,F在线段AB上,点M在线段B1C1上,点N在线段C1D1上,且EF=1,D1N=x,AE=y,M是B1C1的中点,则四面体MNEF的体积( )
8、如图,已知正方体ABCD-A1B1C1D1的棱长为3,点E,F在线段AB上,点M在线段B1C1上,点N在线段C1D1上,且EF=1,D1N=x,AE=y,M是B1C1的中点,则四面体MNEF的体积( )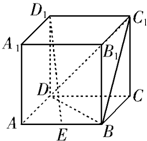 如图,已知正方体ABCD-A1B1C1D1的棱长为2,点E为棱AB的中点.
如图,已知正方体ABCD-A1B1C1D1的棱长为2,点E为棱AB的中点. 如图,已知正方体ABCD-A1B1C1D1的棱长为2,E、F分别是D1C、AB的中点.
如图,已知正方体ABCD-A1B1C1D1的棱长为2,E、F分别是D1C、AB的中点. 如图,已知正方体ABCD-A1B1C1D1的棱长为2,点P,Q,R分别是棱AB,CC1,D1A1的中点.
如图,已知正方体ABCD-A1B1C1D1的棱长为2,点P,Q,R分别是棱AB,CC1,D1A1的中点. (2012•宝山区一模)如图,已知正方体ABCD-A1B1C1D1 的棱长为2,E,F分别是BB1,CD的中点.
(2012•宝山区一模)如图,已知正方体ABCD-A1B1C1D1 的棱长为2,E,F分别是BB1,CD的中点.