题目内容
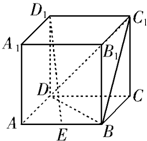 如图,已知正方体ABCD-A1B1C1D1的棱长为2,点E为棱AB的中点.
如图,已知正方体ABCD-A1B1C1D1的棱长为2,点E为棱AB的中点.求:
(1)D1E与平面BC1D所成角的正弦值;
(2)二面角D-BC1-C的余弦值.
分析:(1)延长EB至F使BF=1,连接C1F,则C1F∥D1E,则C1F与平面BC1D所成角等于D1E与平面BC1D所成角θ,计算出F到BC1D的距离h.则sinθ=
(2)取BC1的中点H,连接DH,CH,则∠DHC为二面角D-BC1-C的平面角,在△DHC中利用余弦定理计算即可.
| h |
| C1F |
(2)取BC1的中点H,连接DH,CH,则∠DHC为二面角D-BC1-C的平面角,在△DHC中利用余弦定理计算即可.
解答:解:(1)如图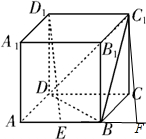
延长EB至F使BF=1,连接C1F,则C1F∥D1E,则C1F与平面BC1D所成角等于D1E与平面BC1D所成角,设为θ,
设F到BC1D的距离为h.,则VC1-DBF=V F-C1BD∴
S△DBF×CC1=
S△DBC1×h,S△DBF=
×BF×DA=1,
S△DBC1=
×8=2
,∴h=
,sinθ=
═
=
=
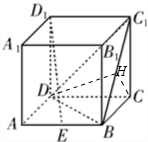
(2)取BC1的中点H,连接DH,CH,∵△DBC1为正三角形,BCC1为等腰直角三角形,∴DH⊥BC 1,CH⊥BC 1
∴∠DHC为二面角D-BC1-C的平面角,设为β,在△DHC中,cosβ=
=
=

延长EB至F使BF=1,连接C1F,则C1F∥D1E,则C1F与平面BC1D所成角等于D1E与平面BC1D所成角,设为θ,
设F到BC1D的距离为h.,则VC1-DBF=V F-C1BD∴
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
S△DBC1=
| ||
| 4 |
| 3 |
| ||
| 3 |
| h |
| C1F |
| h |
| D1E |
| ||||
| 3 |
| ||
| 9 |
(2)取BC1的中点H,连接DH,CH,∵△DBC1为正三角形,BCC1为等腰直角三角形,∴DH⊥BC 1,CH⊥BC 1
∴∠DHC为二面角D-BC1-C的平面角,设为β,在△DHC中,cosβ=
| DH2+HC2- CD2 |
| 2DH×HC |
| 6+2-4 | ||||
2
|
| ||
| 3 |

点评:本题考查线面角、二面角求解,考查化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力

练习册系列答案
相关题目
 8、如图,已知正方体ABCD-A1B1C1D1的棱长为3,点E,F在线段AB上,点M在线段B1C1上,点N在线段C1D1上,且EF=1,D1N=x,AE=y,M是B1C1的中点,则四面体MNEF的体积( )
8、如图,已知正方体ABCD-A1B1C1D1的棱长为3,点E,F在线段AB上,点M在线段B1C1上,点N在线段C1D1上,且EF=1,D1N=x,AE=y,M是B1C1的中点,则四面体MNEF的体积( ) 如图,已知正方体ABCD-A1B1C1D1的棱长为2,E、F分别是D1C、AB的中点.
如图,已知正方体ABCD-A1B1C1D1的棱长为2,E、F分别是D1C、AB的中点. 如图,已知正方体ABCD-A1B1C1D1的棱长为2,点P,Q,R分别是棱AB,CC1,D1A1的中点.
如图,已知正方体ABCD-A1B1C1D1的棱长为2,点P,Q,R分别是棱AB,CC1,D1A1的中点. (2012•宝山区一模)如图,已知正方体ABCD-A1B1C1D1 的棱长为2,E,F分别是BB1,CD的中点.
(2012•宝山区一模)如图,已知正方体ABCD-A1B1C1D1 的棱长为2,E,F分别是BB1,CD的中点.