题目内容
 如图,已知正方体ABCD-A1B1C1D1的棱长为2,点P,Q,R分别是棱AB,CC1,D1A1的中点.
如图,已知正方体ABCD-A1B1C1D1的棱长为2,点P,Q,R分别是棱AB,CC1,D1A1的中点.(1)求证:B1D⊥平面PQR;
(2)设二面角B1-PR-Q的大小为θ,求|cosθ|.
分析:(1)建立空间直角坐标系,用坐标表示向量,利用向量的数量积为0,判断向量垂直,再利用线面垂直的判定定理可以证明;
(2)求出平面B1PR的一个法向量,利用向量的夹角公式,我们可以求出向量的夹角的余弦值,这样,我们就利用求出|cosθ|.
(2)求出平面B1PR的一个法向量,利用向量的夹角公式,我们可以求出向量的夹角的余弦值,这样,我们就利用求出|cosθ|.
解答: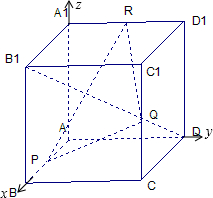 解:(1)建立如图所示的空间直角坐标系,则P(1,0,0),
解:(1)建立如图所示的空间直角坐标系,则P(1,0,0),
Q(2,2,1),R(0,1,2),D(0,2,0),B1(2,0,2)
∴
=(-1,1,2),
=(1,2,1),
=(-2,2,-2)
∴
•
=2+2-4=0,
•
=-2+4-2=0
∴
⊥
,
⊥
∵PR∩PQ=P,PR,PQ⊆平面PQR;
∴B1D⊥平面PQR;
(2)由(1)知,
是平面PQR的一个法向量
设
=(x,y,z)是平面B1PR的一个法向量
∵
=(-1,0,-2)
∴
,∴
取z=1,则x=-2,y=-4
∴平面B1PR的一个法向量为
=(-2,-4,1)
∴cos<
,
> =
=
=-
∴|cosθ|=
 解:(1)建立如图所示的空间直角坐标系,则P(1,0,0),
解:(1)建立如图所示的空间直角坐标系,则P(1,0,0),Q(2,2,1),R(0,1,2),D(0,2,0),B1(2,0,2)
∴
| PR |
| PQ |
| B1D |
∴
| PR |
| B1D |
| PQ |
| B1D |
∴
| PR |
| B1D |
| PQ |
| B1D |
∵PR∩PQ=P,PR,PQ⊆平面PQR;
∴B1D⊥平面PQR;
(2)由(1)知,
| B1D |
设
| n |
∵
| B1P |
∴
|
|
取z=1,则x=-2,y=-4
∴平面B1PR的一个法向量为
| n |
∴cos<
| n |
| B1D |
| ||||
|
|
| 4-8-2 | ||||
2
|
| ||
| 7 |
∴|cosθ|=
| ||
| 7 |
点评:利用空间向量解决立体几何问题优点是减少辅助线的添加,利用代数的方法解决立体几何问题,这是向量的一种创新运用.

练习册系列答案
相关题目
 8、如图,已知正方体ABCD-A1B1C1D1的棱长为3,点E,F在线段AB上,点M在线段B1C1上,点N在线段C1D1上,且EF=1,D1N=x,AE=y,M是B1C1的中点,则四面体MNEF的体积( )
8、如图,已知正方体ABCD-A1B1C1D1的棱长为3,点E,F在线段AB上,点M在线段B1C1上,点N在线段C1D1上,且EF=1,D1N=x,AE=y,M是B1C1的中点,则四面体MNEF的体积( ) 如图,已知正方体ABCD-A1B1C1D1的棱长为2,点E为棱AB的中点.
如图,已知正方体ABCD-A1B1C1D1的棱长为2,点E为棱AB的中点. 如图,已知正方体ABCD-A1B1C1D1的棱长为2,E、F分别是D1C、AB的中点.
如图,已知正方体ABCD-A1B1C1D1的棱长为2,E、F分别是D1C、AB的中点. (2012•宝山区一模)如图,已知正方体ABCD-A1B1C1D1 的棱长为2,E,F分别是BB1,CD的中点.
(2012•宝山区一模)如图,已知正方体ABCD-A1B1C1D1 的棱长为2,E,F分别是BB1,CD的中点.