题目内容
若对任意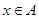 ,
,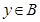 ,(
,(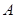 、
、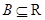 )有唯一确定的
)有唯一确定的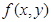 与之对应,称
与之对应,称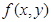 为关于
为关于 、
、 的二元函数. 现定义满足下列性质的二元函数
的二元函数. 现定义满足下列性质的二元函数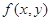 为关于实数
为关于实数 、
、 的广义“距离”:
的广义“距离”:
(1)非负性: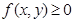 ,当且仅当
,当且仅当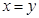 时取等号;
时取等号;
(2)对称性: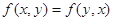 ;
;
(3)三角形不等式: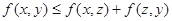 对任意的实数z均成立.
对任意的实数z均成立.
今给出个二元函数:①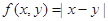 ;②
;②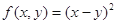 ;③
;③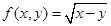 ;④
;④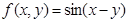 .则能够成为关于的
.则能够成为关于的 、
、 的广义“距离”的函数的所有序号是 .
的广义“距离”的函数的所有序号是 .
(1)
解析试题分析:对于①,f(x,y)=|x-y|≥0满足(1),f(x,y)=|x-y|=f(y,x)=|y-x|满足(2);
f(x,y)=|x-y|=|(x-z)+(z-y)|≤|x-z|+|z-y|=f(x,z)+f(z,y)满足(3)
故①能够成为关于的x、y的广义“距离”的函数;对于②不满足(3);对于③不满足(2);对于④不满足(1)(2),故答案为①
考点:1.函数的概念及其构成要素.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
设 定义如下面数表,
定义如下面数表,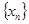 满足
满足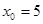 ,且对任意自然数
,且对任意自然数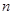 均有
均有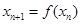 ,则
,则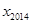 的值为__________________。
的值为__________________。
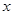 | 1 | 2 | 3 | 4 | 5 |
 | 4 | 1 | 3 | 5 | 2 |
 的定义域是_____________.
的定义域是_____________.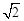 ),则
),则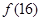 = .
= .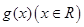 的图像如图所示,关于
的图像如图所示,关于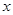 的方程
的方程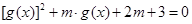 有三个不同的实数解,则
有三个不同的实数解,则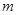 的取值范围是_______________.
的取值范围是_______________.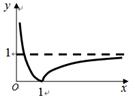
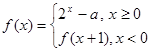 ,若方程
,若方程 有且仅有两个解,则实数
有且仅有两个解,则实数 的取值范围是 .
的取值范围是 .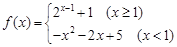 ,若函数
,若函数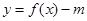 有三个不同的零点,则实数m的取值范围是 .
有三个不同的零点,则实数m的取值范围是 .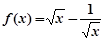 .若
.若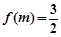 ,则
,则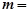 ____.
____.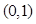 到实数集R的映射过程:区间
到实数集R的映射过程:区间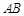 围成一个圆,使两端点A、B恰好重合,如图②;再将这个圆放在平面直角坐标系中,使其圆心在y轴上,点A的坐标为
围成一个圆,使两端点A、B恰好重合,如图②;再将这个圆放在平面直角坐标系中,使其圆心在y轴上,点A的坐标为 ,则m的象就是n,记作
,则m的象就是n,记作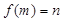 .
.
 ;
; 在定义域
在定义域 上单调递增;
上单调递增;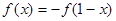 ;
; 的不等式
的不等式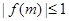 的解集为
的解集为 .
.