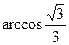题目内容
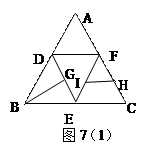
(本小题满分14分)如图,在直三棱柱ABC-A1B1C1中,点D、E分别在边BC、
B1C1上,CD=B1E=AC,ÐA CD=60°.
CD=60°.
求证:(1)BE∥平面AC1D;
(2) 平面ADC1⊥平面BCC1B1.
平面ADC1⊥平面BCC1B1.

B1C1上,CD=B1E=AC,ÐA
 CD=60°.
CD=60°.求证:(1)BE∥平面AC1D;
(2)
 平面ADC1⊥平面BCC1B1.
平面ADC1⊥平面BCC1B1.
证明:(1)由三棱柱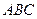 是直三棱柱,得
是直三棱柱,得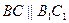 .
.
因为点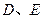 分别边
分别边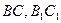 上,
上, ,
,
所以 ,
, .
.
所以 四边形 是平行四形,所以
是平行四形,所以
因为 ,
,
所以
(2)由三棱柱 是直三棱柱,得
是直三棱柱,得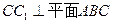
因为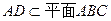 ,所以
,所以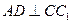
在 中,由
中,由

得
所以
所以 ,即:
,即:
因为 ,
, ,
,
所以
因为 所以
所以 
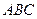 是直三棱柱,得
是直三棱柱,得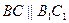 .
.因为点
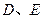 分别边
分别边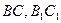 上,
上, ,
,所以
 ,
, .
.所以 四边形
 是平行四形,所以
是平行四形,所以
因为
 ,
,
所以

(2)由三棱柱
 是直三棱柱,得
是直三棱柱,得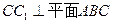
因为
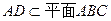 ,所以
,所以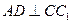
在
 中,由
中,由

得

所以

所以
 ,即:
,即:
因为
 ,
, ,
,
所以

因为
 所以
所以 
略

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案
相关题目
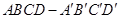 中,
中,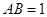 ,
, ,则
,则 两点间的球面距离为
两点间的球面距离为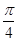

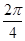

 B=1,BC=a,PA⊥平面ABCD
B=1,BC=a,PA⊥平面ABCD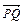 ⊥
⊥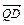 ,说明理由.
,说明理由.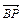 ,
, 时,求点P的位置.
时,求点P的位置.
 B.
B.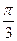 C.
C. D.
D.