题目内容
已知向量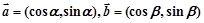 且
且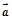 与
与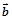 满足关系式:
满足关系式: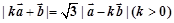 .
.
(1)用k表示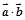 ;
;
(2)证明: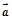 与
与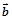 不垂直;
不垂直;
(3)当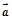 与
与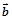 的夹角为
的夹角为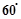 时,求k的值.
时,求k的值.
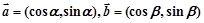 且
且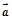 与
与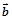 满足关系式:
满足关系式: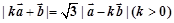 .
.(1)用k表示
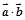 ;
;(2)证明:
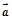 与
与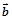 不垂直;
不垂直;(3)当
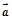 与
与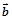 的夹角为
的夹角为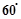 时,求k的值.
时,求k的值. 解:(1)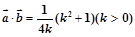 (2)证明:略 (3)k=1
(2)证明:略 (3)k=1
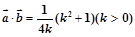 (2)证明:略 (3)k=1
(2)证明:略 (3)k=1本试题主要是考查了向量的数量积公式的运用
(1)利用向量的模长相等,平方法得到数量积的求解。
(2)要证明不垂直,只要证明数量积不为零即可。
(3)利用向量的夹角,和数量积公式,可知参数k的值。
(1)利用向量的模长相等,平方法得到数量积的求解。
(2)要证明不垂直,只要证明数量积不为零即可。
(3)利用向量的夹角,和数量积公式,可知参数k的值。

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目
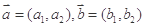 ,定义一种向量积:
,定义一种向量积: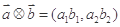 ,
, 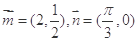 ,且点
,且点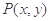 在函数
在函数 的图象上运动,点
的图象上运动,点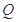 在函数
在函数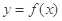 的图象上运动,且点
的图象上运动,且点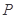 和点
和点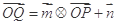 (其中O为坐标原点),则函数
(其中O为坐标原点),则函数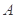 及最小正周期
及最小正周期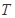 分别为
分别为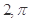
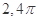
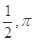
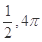
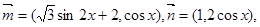 设函数
设函数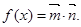
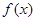 的最小正周期与单调递减区间;
的最小正周期与单调递减区间;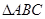 中
中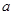 、
、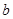 、
、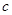 分别是角
分别是角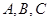 的对边,若
的对边,若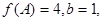
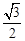 ,求
,求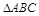 中,设
中,设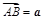 ,
,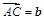 ,
,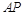 的中点为
的中点为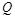 ,
,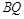 的中点为
的中点为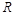 ,
,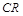 的中点恰为
的中点恰为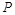 .
.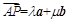 ,求
,求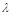 和
和 的值;
的值;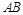 ,
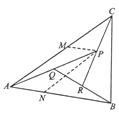
,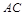 为邻边,
为邻边, 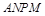 ,
,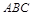 的面积之比
的面积之比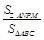 .
.
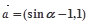 ,
,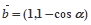 ,
,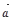 ·
·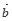 =
= ,
,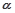 ∈(0,
∈(0,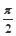 ).
).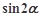 及
及 ,
, 的值;
的值;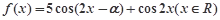 ,求
,求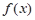 的最小正周期和图象的对称中心坐标;
的最小正周期和图象的对称中心坐标;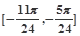 上的值域.
上的值域.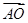 =x
=x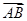 +(1-x)
+(1-x)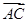 ,则实数x的取值范围是
,则实数x的取值范围是 ,
, ,若
,若 ,则向量
,则向量 与
与 的夹角为( )
的夹角为( )



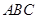 中,
中,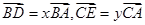 ,
,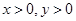 ,且
,且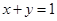 ,则
,则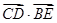 的最大值为( )
的最大值为( )