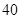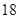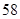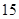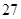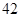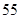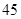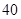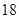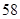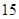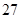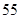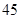题目内容
 某校为了解学生的学科学习兴趣,对初高中学生做了一个喜欢数学和喜欢语文的抽样调查,随机抽取了100名学生,相关的数据如下表所示:
某校为了解学生的学科学习兴趣,对初高中学生做了一个喜欢数学和喜欢语文的抽样调查,随机抽取了100名学生,相关的数据如下表所示:| 数学 | 语文 | 总计 | |
| 初中 | 36 | 14 | 50 |
| 高中 | 24 | 26 | 50 |
| 总计 | 60 | 40 | 100 |
(2)在(1)中抽取的5名学生中任取2名,求恰有1名高中学生的概率.
分析:(1)根据高中学生应该抽取的人数=抽取人数×喜欢数学所占比例即可求出所求;
(2)列举出从5名学生中任取2名的所有可能的情况,然后找出恰有1名高中学生的情况,最后根据古典概型的概率公式解之即可.
(2)列举出从5名学生中任取2名的所有可能的情况,然后找出恰有1名高中学生的情况,最后根据古典概型的概率公式解之即可.
解答:解:(1)由表中数据可知,高中学生应该抽取5×
=2人.…(5分)
(2)记抽取的5名学生中,高中2名学生为A,B,初中3名学生为a,b,c,
则从5名学生中任取2名的所有可能的情况有10种,它们是:(A,B),(A,a),(A,b),(A,c),(B,a),(B,b),(B,c),(a,b),(a,c),(b,c).…(9分)
其中恰有1名高中学生的情况有6种,它们是:(A,a),(A,b),(A,c),(B,a),(B,b),(B,c).…(11分)
故所求概率为
=
.…(12分)
| 24 |
| 60 |
(2)记抽取的5名学生中,高中2名学生为A,B,初中3名学生为a,b,c,
则从5名学生中任取2名的所有可能的情况有10种,它们是:(A,B),(A,a),(A,b),(A,c),(B,a),(B,b),(B,c),(a,b),(a,c),(b,c).…(9分)
其中恰有1名高中学生的情况有6种,它们是:(A,a),(A,b),(A,c),(B,a),(B,b),(B,c).…(11分)
故所求概率为
| 6 |
| 10 |
| 3 |
| 5 |
点评:本题主要考查了古典概型及其概率计算公式,以及列举法的应用,同时考查了运算求解的能力,属于基础题.

练习册系列答案
相关题目
(12分)某校为了解学生的学科学习兴趣,对初高中学生做了一个喜欢数学和喜欢语文的抽样调查,随机抽取了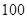 名学生,相关的数据如下表所示:
名学生,相关的数据如下表所示:
|
|
数学 |
语文 |
总计 |
|
初中 |
|
|
|
|
高中 |
|
|
|
|
总计 |
|
|
|
(1) 、用分层抽样的方法从喜欢语文的学生中随机抽取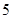 名,高中学生应该抽取几名?
名,高中学生应该抽取几名?
(2) 、在(1)中抽取的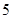 名学生中任取
名学生中任取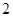 名,求恰有
名,求恰有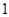 名初中学生的概率.
名初中学生的概率.
某校为了解学生的学科学习兴趣,对初高中学生做了一个喜欢数学和喜欢语文的抽样调查,随机抽取了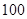 名学生,相关的数据如下表所示:
名学生,相关的数据如下表所示:
|
|
数学 |
语文 |
总计 |
|
初中 |
|
|
|
|
高中 |
|
|
|
|
总计 |
|
|
|
(1) 用分层抽样的方法从喜欢语文的学生中随机抽取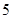 名,高中学生应该抽取几名?
名,高中学生应该抽取几名?
(2) 在(1)中抽取的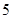 名学生中任取
名学生中任取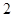 名,求恰有
名,求恰有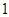 名初中学生的概率.
名初中学生的概率.
某校为了解学生的学科学习兴趣,对初高中学生做了一个喜欢数学和喜欢语文的抽样调查,随机抽取了100名学生,相关的数据如下表所示:
(1)用分层抽样的方法从喜欢数学的学生中随机抽取5名,高中学生应该抽取几名?
(2)在(1)中抽取的5名学生中任取2名,求恰有1名高中学生的概率.
| 数学 | 语文 | 总计 | |
| 初中 | 36 | 14 | 50 |
| 高中 | 24 | 26 | 50 |
| 总计 | 60 | 40 | 100 |
(2)在(1)中抽取的5名学生中任取2名,求恰有1名高中学生的概率.