题目内容
已知函数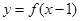 的图象关于点
的图象关于点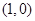 对称,且当
对称,且当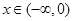 时,
时,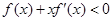 成立(其中
成立(其中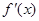 是
是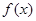 的导函数),若
的导函数),若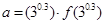 ,
,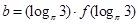 ,
,
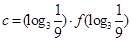 ,则
,则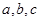 的大小关系是( )
的大小关系是( )
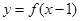 的图象关于点
的图象关于点 对称,且当
对称,且当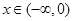 时,
时,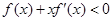 成立(其中
成立(其中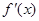 是
是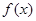 的导函数),若
的导函数),若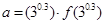 ,
,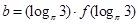 ,
,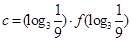 ,则
,则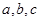 的大小关系是( )
的大小关系是( )A. | B. | C. | D. |
C
解:∵当x∈(-∞,0)时不等式f(x)+xf′(x)<0成立
即:(xf(x))′<0,
∴xf(x)在 (-∞,0)上是减函数.
又∵函数y=f(x-1)的图象关于点(1,0)对称,
∴函数y=f(x)的图象关于点(0,0)对称,
∴函数y=f(x)是定义在R上的奇函数
∴xf(x)是定义在R上的偶函数
∴xf(x)在 (0,+∞)上是增函数.
又∵30.3>1>log π 3>0>log 3 1 /9 =-2,
2="-" log 3 1 /9>30.3>1>log π 3 >0.
∴(-log 3 1 /9 )•f(-log 3 1 /9 )>30.3•f(30.3)>(logπ3)•f(logπ3)
即(log 3 1 /9 )•f(log 3 1 /9 )>30.3•f(30.3)>(logπ3)•f(logπ3)
即:c>a>b
故选C.
即:(xf(x))′<0,
∴xf(x)在 (-∞,0)上是减函数.
又∵函数y=f(x-1)的图象关于点(1,0)对称,
∴函数y=f(x)的图象关于点(0,0)对称,
∴函数y=f(x)是定义在R上的奇函数
∴xf(x)是定义在R上的偶函数
∴xf(x)在 (0,+∞)上是增函数.
又∵30.3>1>log π 3>0>log 3 1 /9 =-2,
2="-" log 3 1 /9>30.3>1>log π 3 >0.
∴(-log 3 1 /9 )•f(-log 3 1 /9 )>30.3•f(30.3)>(logπ3)•f(logπ3)
即(log 3 1 /9 )•f(log 3 1 /9 )>30.3•f(30.3)>(logπ3)•f(logπ3)
即:c>a>b
故选C.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
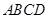 中,
中,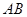 ∥
∥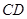 ,
,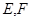 是线段
是线段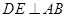 ,
,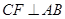 ,
,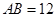 ,
,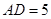 ,
,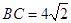 ,
,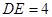 .现将△
.现将△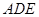 ,△
,△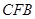 分别沿
分别沿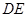 ,
,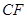 折起,使两点
折起,使两点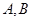 重合于点
重合于点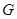 ,得到多面体
,得到多面体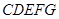 (1)求证:平面
(1)求证:平面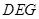
 平面
平面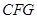 ;(2)求多面体
;(2)求多面体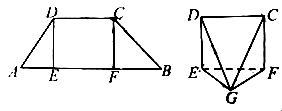
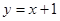
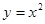
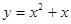
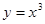
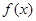 是奇函数,则
是奇函数,则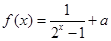 ,
,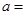 。
。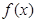 是定义在
是定义在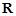 上的奇函数,且当
上的奇函数,且当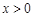 时,
时,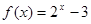 ,则
,则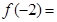 .
.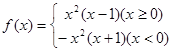 ,判断它的奇偶性。
,判断它的奇偶性。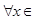 R,函数
R,函数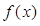 都满足
都满足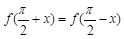 ,且当
,且当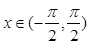 时,
时,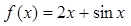 ,则( )
,则( )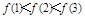
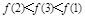
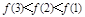
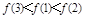
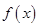 是
是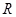 上的奇函数,且当
上的奇函数,且当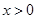 时,
时,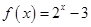 ,则
,则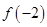 等于( )
等于( )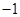
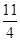
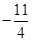
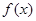 (x∈R)为奇函数,
(x∈R)为奇函数,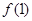 =
=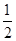 ,
,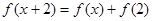 ,则
,则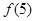 =( )
=( )