Question

（2012•资阳一模）设函数f（x）=

21-x，x≤0 f(x-1)，x＞0

若关于x的方程f（x）=x+a有且只有两个实根，则实数a的范围是（　　）

A．（2，4）

B．[3，4]

C．（-∞，3]

D．[3，+∞）

Answer 1

分析：作出函数y=f（x）和y=x+a的图象，利用两个函数的图象确定a的取值范围即可．

解答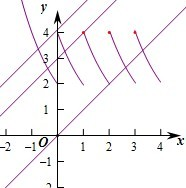：解：由f（x）=x+a，设函数y=f（x）和y=x+a，
当0＜x≤1，-1＜x-1≤0，
此时，f（x）=f（x-1）=2^1-（x-1）=2^2-x，
当x＞0时，函数f（x）的周期为1，
作出函数f（x）的图象如图：
∵f（-1）=2²=4，
∴f（1）=f（0）=f（-1）=4，
要使方程f（x）=x+a有且只有两个实根，
则由图象可知3≤a≤4．
故选：B．

点评：本题主要考查函数图象的应用，将方程根的个数转化为函数交点个数是解决本题的关键，利用数形结合是解决此问题的突破点．