题目内容
【题目】如图,在平面直角坐标系xOy中,焦点在x轴上的椭圆C: ![]() =1经过点(b,2e),其中e为椭圆C的离心率.过点T(1,0)作斜率为k(k>0)的直线l交椭圆C于A,B两点(A在x轴下方).
=1经过点(b,2e),其中e为椭圆C的离心率.过点T(1,0)作斜率为k(k>0)的直线l交椭圆C于A,B两点(A在x轴下方).
(1)求椭圆C的标准方程;
(2)过点O且平行于l的直线交椭圆C于点M,N,求 ![]() 的值;
的值;
(3)记直线l与y轴的交点为P.若 ![]() =
= ![]()
![]() ,求直线l的斜率k.
,求直线l的斜率k.
【答案】
(1)
解:因为椭圆椭圆C: ![]() =1经过点(b,2e)所以
=1经过点(b,2e)所以 ![]() .
.
因为e2= ![]() ,所以
,所以 ![]() ,
,
又∵a2=b2+c2, ![]() ,解得b2=4或b2=8(舍去).
,解得b2=4或b2=8(舍去).
所以椭圆C的方程为 ![]()
(2)
解:设A(x1,y1),B(x2,y2).
因为T(1,0),则直线l的方程为y=k(x﹣1).
联立直线l与椭圆方程 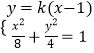 ,消去y,得(2k2+1)x2﹣4k2x+2k2﹣8=0,
,消去y,得(2k2+1)x2﹣4k2x+2k2﹣8=0,
所以x1+x2= ![]() ,x1x2=
,x1x2= ![]() .
.
因为MN∥l,所以直线MN方程为y=kx,
联立直线MN与椭圆方程 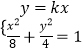
消去y得(2k2+1)x2=8,
解得x2= ![]()
因为MN∥l,所以 ![]()
因为(1﹣x1)(x2﹣1)=﹣[x1x2﹣(x1+x2)+1]= ![]() .
.
(xM﹣xN)2=4x2= ![]() .
.
所以 ![]() =
= ![]()
(3)
解:在y=k(x﹣1)中,令x=0,则y=﹣k,所以P(0,﹣k),
从而 ![]() ,
,
∵ ![]() =
= ![]()
![]() ,
, ![]() …①
…①
由(2)知 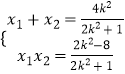 …②
…②
由①②得 ![]() 50k4﹣83k2﹣34=0,解得k2=2或k2=﹣
50k4﹣83k2﹣34=0,解得k2=2或k2=﹣ ![]() (舍).
(舍).
又因为k>0,所以k= ![]()
【解析】(1)由题意得e2= ![]() ,
, ![]() .又a2=b2+c2 ,
.又a2=b2+c2 , ![]() ,解得b2;(2)设A(x1 , y1),B(x2 , y2).设直线l的方程为y=k(x﹣1).
,解得b2;(2)设A(x1 , y1),B(x2 , y2).设直线l的方程为y=k(x﹣1).
联立直线l与椭圆方程 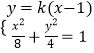 ,消去y,得(2k2+1)x2﹣4k2x+2k2﹣8=0,可设直线MN方程为y=kx,联立直线MN与椭圆方程
,消去y,得(2k2+1)x2﹣4k2x+2k2﹣8=0,可设直线MN方程为y=kx,联立直线MN与椭圆方程 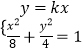 ,消去y得(2k2+1)x2=8,由MN∥l,得
,消去y得(2k2+1)x2=8,由MN∥l,得 ![]()
由(1﹣x1)(x2﹣1)=﹣[x1x2﹣(x1+x2)+1]= ![]() .得(xM﹣xN)2=4x2=
.得(xM﹣xN)2=4x2= ![]() .即可. (3)在y=k(x﹣1)中,令x=0,则y=﹣k,所以P(0,﹣k),从而
.即可. (3)在y=k(x﹣1)中,令x=0,则y=﹣k,所以P(0,﹣k),从而 ![]() ,由
,由 ![]() =
= ![]()
![]() 得
得 ![]() …①,由(2)知
…①,由(2)知 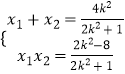 …②由①②得
…②由①②得 ![]() 50k4﹣83k2﹣34=0,解得k2
50k4﹣83k2﹣34=0,解得k2
【考点精析】认真审题,首先需要了解椭圆的标准方程(椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() ).
).

 阅读快车系列答案
阅读快车系列答案【题目】为了巩固全国文明城市创建成果,今年吉安市开展了拆除违章搭建铁皮棚专项整治行为.为了了解市民对此项工作的“支持”与“反对”态度,随机从存在违章搭建的户主中抽取了男性、女性共![]() 名进行调查,调查结果如下:
名进行调查,调查结果如下:
支持 | 反对 | 合计 | |
男性 |
|
|
|
女性 |
|
|
|
合计 |
|
|
|
(1)根据以上数据,判断是否有![]() 的把握认为对此项工作的“支持”与“反对”态度与“性别”有关;
的把握认为对此项工作的“支持”与“反对”态度与“性别”有关;
(2)现从参与调查的女户主中按分层抽样的方法抽取![]() 人进行调查,分别求出所抽取的
人进行调查,分别求出所抽取的![]() 人中持“支持”和“反对”态度的人数;
人中持“支持”和“反对”态度的人数;
(3)现从(2)中所抽取的![]() 人中,再随机抽取
人中,再随机抽取![]() 人赠送小品,求恰好抽到
人赠送小品,求恰好抽到![]() 人持“支持”态度的概率?
人持“支持”态度的概率?
参考公式:![]() ,其中
,其中![]() .
.
参考数据:
|
|
|
|
|
|
|
|


