题目内容
某集团公司举办一次募捐爱心演出,有1000人参加,每人一张门票,每张100元。在演出过程中穿插抽奖活动,第一轮抽奖从这1000张票根中随机抽取10张,其持有者获得价值1000元的奖品,并参加第二轮抽奖活动。第二轮抽奖由第一轮获奖者独立操作按钮,电脑随机产生两个数 (
(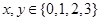 ),满足
),满足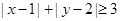 电脑显示“中奖”,且抽奖者获得特等奖奖金;否则电脑显示“谢谢”,则不中奖。
电脑显示“中奖”,且抽奖者获得特等奖奖金;否则电脑显示“谢谢”,则不中奖。
(1)已知小明在第一轮抽奖中被抽中,求小明在第二轮抽奖中获奖的概率;
(2)若该集团公司望在此次活动中至少获得61875元的收益,则特等奖奖金最高可设置成多少元?
(1)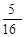 (2)a≤9900
(2)a≤9900
解析试题分析:(Ⅰ)从0,1,2,3四个数字中有重复取2个数字,其基本事件有(0,0),(0,1),(0,2),(0,3),(1,0),(1,1),(1,2),(1,3),(2,0),(2,1),(2,2),(2,3),(3,0),(3,1),(3,2),(3,3)共 16 个.
设“小明在第二轮抽奖中获奖”为事件A,且事件A所包含的基本事件有(0,0),(2,0),(3,0),(3,1),(3,3)共5个,∴P(A)=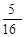 .
.
(Ⅱ)设特等奖奖金为a元,一个人参加此次活动的收益为ξ,则ξ的可能取值为-100,900,a.
P(ξ=-100)= ,P(ξ=900)=
,P(ξ=900)=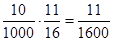 ,P(ξ="a)="
,P(ξ="a)=" 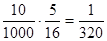 .
.
∴ξ的分布列为
∴ξ -100 900 a P 
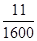
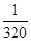
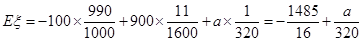 .
.
∴该集团公司收益的期望为 ,
,
由题意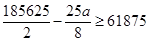 ,解得a≤9900.
,解得a≤9900.
故特等奖奖金最高可设置成9900元.
考点:古典概型和分布列
点评:主要是考查了古典概型概率和分布列的运用,属于中档题。

每一个父母都希望自己的孩子能升上比较理想的中学,于是就催生了“择校热”,这样“择校”的结果就导致了学生在路上耽误的时间增加了.若某生由于种种原因,每天只能6:15骑车从家出发到学校,途经5个路口,这5个路口将家到学校分成了6个路段,每个路段的骑车时间是10分钟(通过路口的时间忽略不计),假定他在每个路口遇见红灯的概率均为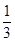 ,且该生只在遇到红灯或到达学校才停车.对每个路口遇见红灯的情况统计如下:
,且该生只在遇到红灯或到达学校才停车.对每个路口遇见红灯的情况统计如下:
| 红灯 | 1 | 2 | 3 | 4 | 5 |
| 等待时间(秒) | 60 | 60 | 90 | 30 | 90 |
(2)设
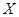 表示该学生第一次停车时已经通过的路口数,求它的分布列与期望.
表示该学生第一次停车时已经通过的路口数,求它的分布列与期望. 某小组共有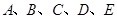 五位同学,他们的身高(单位:米)以及体重指标(单位:千克/米2)
五位同学,他们的身高(单位:米)以及体重指标(单位:千克/米2)
如下表所示:
| | A | B | C | D | E |
| 身高 | 1.69 | 1.73 | 1.75 | 1.79 | 1.82 |
| 体重指标 | 19.2 | 25.1 | 18.5 | 23.3 | 20.9 |
(Ⅰ)从该小组身高低于
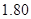 的同学中任选
的同学中任选 人,求选到的
人,求选到的 人身高都在
人身高都在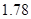 以下的概率
以下的概率(Ⅱ)从该小组同学中任选
 人,求选到的
人,求选到的 人的身高都在
人的身高都在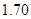 以上且体重指标都在
以上且体重指标都在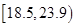 中的概率.
中的概率. 某工厂有甲、乙两个生产小组,每个小组各有四名工人,某天该厂每位工人的生产情况如下表.
| | 员工号 | 1 | 2 | 3 | 4 |
| 甲组 | 件数 | 9 | 11 | 1l | 9 |
| | 员工号 | 1 | 2 | 3 | 4 |
| 乙组 | 件数 | 9 | 8 | 10 | 9 |
(2)求乙组员工生产件数的平均数和方差;
(3)分别从甲、乙两组中随机选取一名员工的生产件数,求这两名员工的生产总件数为19的概率.
(注:方差
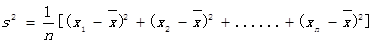 ,其中
,其中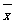 为x1,x2, ,xn的平均数)
为x1,x2, ,xn的平均数)  层第
层第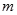 个竖直通道(从左至右)的概率为
个竖直通道(从左至右)的概率为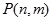 ,某研究性学习小组经探究发现小弹子落入第
,某研究性学习小组经探究发现小弹子落入第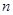 层的第
层的第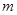 个通道的次数服从二项分布,请你解决下列问题.
个通道的次数服从二项分布,请你解决下列问题.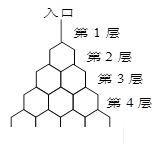
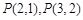 及
及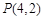 的值,并猜想
的值,并猜想 ,其中
,其中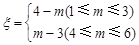 ,试求
,试求 位学生,每次活动均需该系
位学生,每次活动均需该系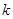 位学生参加(
位学生参加(
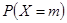 取得最大值的整数
取得最大值的整数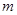 .
. ,乙每次击中目标的概率为
,乙每次击中目标的概率为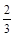
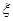 为取出的3个球中白色球的个数,求
为取出的3个球中白色球的个数,求