题目内容
17.设F是抛物线C:y2=12x的焦点,A、B、C为抛物线上不同的三点,若$\overrightarrow{FA}+\overrightarrow{FB}+\overrightarrow{FC}=\overrightarrow 0$,则|FA|+|FB|+|FC|=( )| A. | 3 | B. | 9 | C. | 12 | D. | 18 |
分析 设A(x1,y1),B(x2,y2),C(x3,y3),由已知条件推导出x1+x2+x3=9,根据$\overrightarrow{FA}+\overrightarrow{FB}+\overrightarrow{FC}=\overrightarrow 0$,
得出点F(3,0)是△ABC重心,运用重心的坐标公式得出:x1+x2+x3=9,再根据抛物线的定义得出|FA|+|FB|+|FC|=x1+3+x2+3+x3+3,整体求解即可.
解答 解:设A(x1,y1),B(x2,y2),C(x3,y3)
抛物线y2=12x焦点坐标F(3,0),准线方程:x=-3,
∵$\overrightarrow{FA}+\overrightarrow{FB}+\overrightarrow{FC}=\overrightarrow 0$,
∴点F(3,0)是△ABC重心,
∴x1+x2+x3=9,y1+y2+y3=0,
而|$\overrightarrow{FA}$|=x1-(-3)=x1+3,
|$\overrightarrow{FB}$|=x2-(-3)=x2+3,
|$\overrightarrow{FC}$|=x3-(-3)=x3+3,
∴|FA|+|FB|+|FC|=x1+3+x2+3+x3+3
=(x1+x2+x3)+9=9+9=18.
故选:D.
点评 本题考查抛物线的简单性质的应用,是中档题,解题时要认真审题,注意三角形重心性质的灵活运用

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案
相关题目
12.直线l与直线x-$\sqrt{3}$y+1=0垂直,则直线l的斜率为( )
| A. | $\frac{\sqrt{3}}{3}$ | B. | -$\frac{\sqrt{3}}{3}$ | C. | $\sqrt{3}$ | D. | -$\sqrt{3}$ |
9.函数y=|x-1|的图象( )
| A. | 关于直线x=1对称 | B. | 关于y轴对称 | ||
| C. | 关于直线x=-1对称 | D. | 不是轴对称图形 |
6.下列命题中正确的是( )
| A. | 命题“?x∈R,x2-x≤0”的否定是“?x∈R,x2-x≥0” | |
| B. | 命题“p∧q为真”是命题“p∨q为真”的必要不充分条件 | |
| C. | 若“am2≤bm2,则a≤b”的否命题为真 | |
| D. | 若实数x,y∈[-1,1],则点(x,y)所构成的平面区域为π |
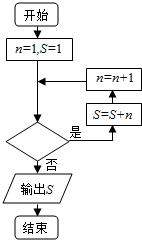 已知数列{an}中,a1=1,an+1=an+n,若利用如图所示的程序框图计算该数列的第10项的值S,则判断框内的条件是n≤9或n<10.
已知数列{an}中,a1=1,an+1=an+n,若利用如图所示的程序框图计算该数列的第10项的值S,则判断框内的条件是n≤9或n<10.