题目内容

关于x的方程sin2x+cosx+a=0有实根，则实数a的取值范围是
 
．
分析：先将原方程转化为：a=-sin2x-cosx，再用同角三角函数基本关系式中的平方关系转化为a=cos2x-cosx+1，再设cosx=t，t∈[-1，1]，
转化为二次函数a=t2-t-1求解．
解答：解：将原方程转化为：a=-sin2x-cosx=cos2x-cosx-1，
设cosx=t，t∈[-1，1]，
则a=t2-t-1=（t-
1
2
）2-
5
4
∈[-
5
4
，1]
故答案为：[-
5
4
，1]；
点评：本题主要考查换元法和方程与函数的转化．
练习册系列答案
相关题目
已知向量
a
=(cos2ωx-sin2ωx，sinωx)，
b
=(
3
，2cosωx)，设函数f(x)=
a
•
b
(x∈R)的图象关于直线x=
π
2
对称，其中ω为常数，且ω∈（0，1）．
（Ⅰ）求函数f（x）的表达式；
（Ⅱ）若将y=f（x）图象上各点的横坐标变为原来的
1
6
，再将所得图象向右平移
π
3
个单位，纵坐标不变，得到y=h（x）的图象，若关于x的方程h（x）+k=0在区间[0，
π
2
]上有且只有一个实数解，求实数k的取值范围．
（2012•上饶一模）请在下列两题中任选一题作答，（如果两题都做，则按所做的第一题评分）
（A）曲线C1的极坐标方程为ρsin2θ=cosθ，曲线C2的参数方程为
x=3-t
y+t=1
，以极点为原点，极轴为x轴正半轴建立直角坐标系，则曲线C1与曲线C2有
2
2
个公共点．
（B）关于x的不等式：|x-1|-|x-2|≤a的解集不是空集，则实数a的范围为
a≥-1
a≥-1
．

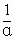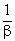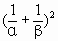关于x的方程x2＋x·sin2θ－sinθcotθ＝0的两根为α，β，且0＜θ＜2π，若数列1，(＋)，，…的前100项和为0，

(文)求sinθ的值．

(理)求θ的值．
已知向量
a
=(cos2ωx-sin2ωx，sinωx)，
b
=(
3
，2cosωx)，设函数f(x)=
a
•
b
(x∈R)的图象关于直线x=
π
2
对称，其中ω为常数，且ω∈（0，1）．
（Ⅰ）求函数f（x）的表达式；
（Ⅱ）若将y=f（x）图象上各点的横坐标变为原来的
1
6
，再将所得图象向右平移
π
3
个单位，纵坐标不变，得到y=h（x）的图象，若关于x的方程h（x）+k=0在区间[0，
π
2
]上有且只有一个实数解，求实数k的取值范围．
请在下列两题中任选一题作答，（如果两题都做，则按所做的第一题评分）
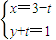（A）曲线C1的极坐标方程为ρsin2θ=cosθ，曲线C2的参数方程为，以极点为原点，极轴为x轴正半轴建立直角坐标系，则曲线C1与曲线C2有    个公共点．
（B）关于x的不等式：|x-1|-|x-2|≤a的解集不是空集，则实数a的范围为    ．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网