题目内容
请在下列两题中任选一题作答,(如果两题都做,则按所做的第一题评分)(A)曲线C1的极坐标方程为ρsin2θ=cosθ,曲线C2的参数方程为
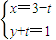 ,以极点为原点,极轴为x轴正半轴建立直角坐标系,则曲线C1与曲线C2有 个公共点.
,以极点为原点,极轴为x轴正半轴建立直角坐标系,则曲线C1与曲线C2有 个公共点.(B)关于x的不等式:|x-1|-|x-2|≤a的解集不是空集,则实数a的范围为 .
【答案】分析:A、先将方程化为直角坐标方程、普通方程,联立,即可求得结论;
B、可设f(x)=|x-1|-|x-2|,然后求其最小值,利用关于x的不等式:|x-1|-|x-2|≤a的解集不是空集,即可求得实数a的范围.
解答:A、解:曲线C1的极坐标方程为ρsin2θ=cosθ,直角坐标方程为y2=x;曲线C2的参数方程为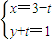 ,普通方程为y=x-2,两方程联立,消去x可得y2=y+2,所以y=2或y=-1,故曲线C1与曲线C2有2个公共点;
,普通方程为y=x-2,两方程联立,消去x可得y2=y+2,所以y=2或y=-1,故曲线C1与曲线C2有2个公共点;
B、解:设f(x)=|x-1|-|x-2|
当x<1时,f(x)=-(x-1)+(x-2)=-1,
当x>2,f(x)=(x-1)-(x-2)=1,
当1≤x≤2,f(x)=(x-1)+(x-2)=2x-3,故此时有-1≤f(x)=2x-3≤1.
综上所述f(x)=|x-1|-|x-2|的最小值为-1,
∵关于x的不等式:|x-1|-|x-2|≤a的解集不是空集,
∴a≥-1
故答案为:2;a≥-1.
点评:本题是选做题,考查坐标系与参数方程,考查不等式,正确转化方程,求函数的最值是关键.
B、可设f(x)=|x-1|-|x-2|,然后求其最小值,利用关于x的不等式:|x-1|-|x-2|≤a的解集不是空集,即可求得实数a的范围.
解答:A、解:曲线C1的极坐标方程为ρsin2θ=cosθ,直角坐标方程为y2=x;曲线C2的参数方程为
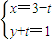 ,普通方程为y=x-2,两方程联立,消去x可得y2=y+2,所以y=2或y=-1,故曲线C1与曲线C2有2个公共点;
,普通方程为y=x-2,两方程联立,消去x可得y2=y+2,所以y=2或y=-1,故曲线C1与曲线C2有2个公共点;B、解:设f(x)=|x-1|-|x-2|
当x<1时,f(x)=-(x-1)+(x-2)=-1,
当x>2,f(x)=(x-1)-(x-2)=1,
当1≤x≤2,f(x)=(x-1)+(x-2)=2x-3,故此时有-1≤f(x)=2x-3≤1.
综上所述f(x)=|x-1|-|x-2|的最小值为-1,
∵关于x的不等式:|x-1|-|x-2|≤a的解集不是空集,
∴a≥-1
故答案为:2;a≥-1.
点评:本题是选做题,考查坐标系与参数方程,考查不等式,正确转化方程,求函数的最值是关键.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
 (请在下列两题中任选一题作答,如果多做,则按所做的第一题评分)
(请在下列两题中任选一题作答,如果多做,则按所做的第一题评分)