题目内容
关于x的方程x2+x·sin2θ-sinθcotθ=0的两根为α,β,且0<θ<2π,若数列1,(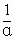 +
+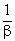 ),
),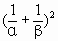 ,…的前100项和为0,
,…的前100项和为0,
(文)求sinθ的值.
(理)求θ的值.
答案:
解析:
解析:
|
∵ a1=1,由等比数列前n项和公式为S100= ∴(2sinθ)100=1,∴2sinθ=-1 (当2sinθ=1时 S100≠0), (文)∴sinθ= (理)又△=(sin2θ)2+4sinθcotθ=4cosθ(1+sin2θcosθ)>0, 而1+sin2θcosθ>0,∴cosθ>0,∴θ= |

练习册系列答案
 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
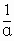 +
+ =
= =
=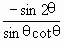 =2sinθ ∴q=2sinθ,
=2sinθ ∴q=2sinθ,
 (2013•宿迁一模)【选做题】本题包括A、B、C、D四小题,请选定其中两题,并在相应的答题区域内作答.若多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤.
(2013•宿迁一模)【选做题】本题包括A、B、C、D四小题,请选定其中两题,并在相应的答题区域内作答.若多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤. 选作题,本题包括A、B、C、D四小题,请选定其中两题,并在相应的答题区域内作答.若多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤.
选作题,本题包括A、B、C、D四小题,请选定其中两题,并在相应的答题区域内作答.若多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤.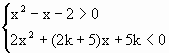 的整数解的集合为{-2},求实数k的取值范围.
的整数解的集合为{-2},求实数k的取值范围.