题目内容
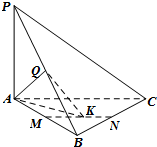
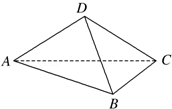
如图,圆锥顶点为P,底面圆心为O,其母线与底面所成的角为22.5°,AB和CD是底面圆O上的两条平行的弦,轴OP与平面PCD所成的角为60°.

(1)证明:平面PAB与平面PCD的交线平行于底面;
(2)求cos∠COD.

(1)证明:平面PAB与平面PCD的交线平行于底面;
(2)求cos∠COD.
(1)见解析 (2)17-12

(1)证明 设平面PAB与平面PCD的交线为l.

因为AB∥CD,AB不在平面PCD内,所以AB∥平面PCD.
又因为AB?平面PAB,平面PAB与平面PCD的交线为l,所以AB∥l.
由直线AB在底面上而l在底面外可知,l与底面平行.
(2)设CD的中点为F,连接OF,PF.
由圆的性质,知∠COD=2∠COF,OF⊥CD.
因为OP⊥底面,CD?底面,所以OP⊥CD.
又OP∩OF=O,故CD⊥平面OPF.
又CD?平面PCD,因此平面OPF⊥平面PCD,从而直线OP在平面PCD上的射影为直线PF,故∠OPF为OP与平面PCD所成的角.由题设,∠OPF=60°.
设OP=h,则OF=OP·tan∠OPF=h·tan 60°= h.
h.
根据题设有∠OCP=22.5°,得
OC= =
=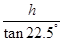 .
.
由1=tan 45°=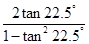 和tan 22.5°>0,
和tan 22.5°>0,
可解得tan 22.5°= -1,
-1,
因此OC=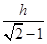 =(
=( +1)h.
+1)h.
在Rt△OCF中,cos∠COF=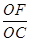 =
=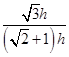 =
=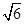 -
- ,
,
故cos∠COD=cos(2∠COF)=2cos2∠COF-1=2(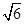 -
- )2-1=17-12
)2-1=17-12 .
.

因为AB∥CD,AB不在平面PCD内,所以AB∥平面PCD.
又因为AB?平面PAB,平面PAB与平面PCD的交线为l,所以AB∥l.
由直线AB在底面上而l在底面外可知,l与底面平行.
(2)设CD的中点为F,连接OF,PF.
由圆的性质,知∠COD=2∠COF,OF⊥CD.
因为OP⊥底面,CD?底面,所以OP⊥CD.
又OP∩OF=O,故CD⊥平面OPF.
又CD?平面PCD,因此平面OPF⊥平面PCD,从而直线OP在平面PCD上的射影为直线PF,故∠OPF为OP与平面PCD所成的角.由题设,∠OPF=60°.
设OP=h,则OF=OP·tan∠OPF=h·tan 60°=
 h.
h.根据题设有∠OCP=22.5°,得
OC=
 =
=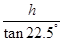 .
.由1=tan 45°=
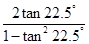 和tan 22.5°>0,
和tan 22.5°>0,可解得tan 22.5°=
 -1,
-1,因此OC=
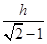 =(
=( +1)h.
+1)h.在Rt△OCF中,cos∠COF=
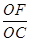 =
=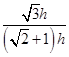 =
=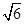 -
- ,
,故cos∠COD=cos(2∠COF)=2cos2∠COF-1=2(
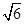 -
- )2-1=17-12
)2-1=17-12 .
.
练习册系列答案
相关题目
 的底面为菱形,
的底面为菱形,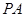
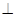 面
面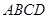 ,且
,且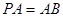 ,
,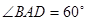 ,
,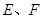 分别是
分别是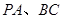 的中点.
的中点.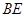 ∥平面
∥平面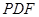 ;
;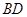 作一平面交棱
作一平面交棱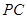 于点
于点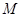 ,若二面角
,若二面角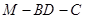 的大小为
的大小为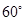 ,求
,求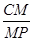 的值.
的值.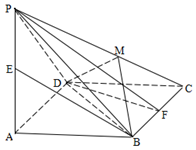
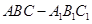 中,
中,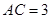 ,
,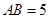 ,
,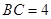 ,
,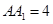 ,点
,点 是
是 的中点.
的中点.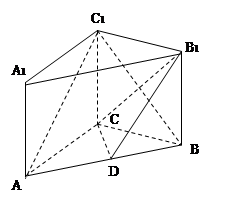
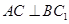 ;
; 
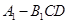 的体积.
的体积.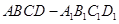 中,
中, 是
是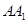 的中点.
的中点.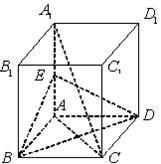
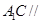 平面
平面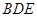 ;
;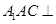 平面
平面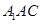 所成角的正弦值.
所成角的正弦值.