题目内容
9.某几何体的三视图如图所示,则该几何体的体积为( )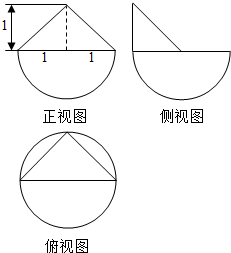
| A. | $\frac{2π+1}{3}$ | B. | $\frac{2π+3}{3}$ | C. | $\frac{4π+1}{3}$ | D. | $\frac{4π+3}{3}$ |
分析 根据几何体的三视图,得出该几何体是半球体与三棱锥的组合体,结合图中数据求出它的体积.
解答 解:根据几何体的三视图,得;
该几何体的下部是半球体,上部是三棱锥,
且半球体的半径为1,三棱锥的底面为直角三角形,高为1;
所以该几何体的体积为
V=$\frac{1}{2}$×$\frac{4}{3}$π×13+$\frac{1}{3}$×$\frac{1}{2}$×2×1×1=$\frac{2π+1}{3}$.
故选:A.
点评 本题考查了空间几何体三视图的应用问题,解题的关键是根据三视图得出几何体的结构特征,是基础题目.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
19.设O为△ABC的外心,且$\overrightarrow{OA}+\overrightarrow{OB}+\sqrt{3}\overrightarrow{OC}=\overrightarrow 0$,则△ABC的内角C=( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
20.已知A(1,2,3)、B(2,1,2)、C(1,1,2),O为坐标原点,点D在直线OC上运动,则当$\overrightarrow{DA}$•$\overrightarrow{DB}$取最小值时,点D的坐标为( )
| A. | ($\frac{4}{3}$,$\frac{4}{3}$,$\frac{4}{3}$) | B. | ($\frac{8}{3}$,$\frac{4}{3}$,$\frac{8}{3}$) | C. | ($\frac{4}{3}$,$\frac{4}{3}$,$\frac{8}{3}$) | D. | ($\frac{8}{3}$,$\frac{8}{3}$,$\frac{4}{3}$) |
19.一条直线不与坐标轴平行或重合,则它的方程( )
| A. | 可以写成两点式或截距式 | B. | 可以写成两点式或斜截式或点斜式 | ||
| C. | 可以写成点斜式或截距式 | D. | 可以写成两点式或截距式或点斜式 |
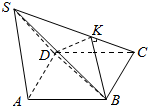 如图,ABCD是正方形,SA⊥平面ABCD,BK⊥SC于点K,连接DK,求证:
如图,ABCD是正方形,SA⊥平面ABCD,BK⊥SC于点K,连接DK,求证: