题目内容
14.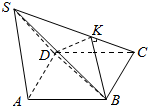 如图,ABCD是正方形,SA⊥平面ABCD,BK⊥SC于点K,连接DK,求证:
如图,ABCD是正方形,SA⊥平面ABCD,BK⊥SC于点K,连接DK,求证:(1)平面SBC⊥平面KBD;
(2)平面SBC不垂直于平面SDC.
分析 (1)连接AC,由已知推导出BD⊥平面SAC,从而SC⊥平面KBD,由此能证明平面SBC⊥平面KBD.
(2)假设平面SBC⊥平面SDC,由已知推导出AB⊥SB,这与∠SBA是Rt△SAB的一个锐角矛盾,故假设不成立,从而得到平面SBC不垂直于平面SDC.
解答 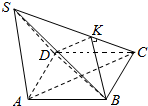 证明:(1)连接AC,∵四边形ABCD是正方形,
证明:(1)连接AC,∵四边形ABCD是正方形,
∴AC⊥BD.又SA⊥平面ABCD,∴SA⊥BD,
∴BD⊥平面SAC,∴SC⊥BD.
又∵SC⊥BK,∴SC⊥平面KBD.
又SC?平面SBC,∴平面SBC⊥平面KBD.
(2)假设平面SBC⊥平面SDC.
∵BK⊥SC,∴BK⊥平面SDC.
∵DC?平面SDC,∴BK⊥DC,
又AB∥CD,∴BK⊥AB.
∵ABCD是正方形,AB⊥BC,
∴AB⊥平面SBC,又SB?平面SBC,
∴AB⊥SB,这与∠SBA是Rt△SAB的一个锐角矛盾,故假设不成立.
∴原结论成立,即平面SBC不垂直于平面SDC.
点评 本题考查面面垂直的证明,考查平面不垂直的证明,是中档题,解题时要注意反证法的合理运用,注意空间思维能力的培养.

练习册系列答案
 目标测试系列答案
目标测试系列答案
相关题目
9.某几何体的三视图如图所示,则该几何体的体积为( )
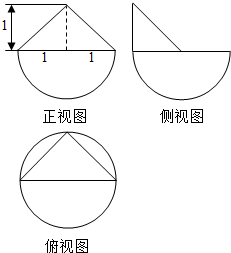

| A. | $\frac{2π+1}{3}$ | B. | $\frac{2π+3}{3}$ | C. | $\frac{4π+1}{3}$ | D. | $\frac{4π+3}{3}$ |
4.若圆锥的高等于底面直径,则它的底面积与侧面积之比为( )
| A. | 1:2 | B. | 1:$\sqrt{3}$ | C. | 1:$\sqrt{5}$ | D. | $\sqrt{3}$:2 |
 如图,已知瞭望塔BA的高度为40m,为测得古塔DC的高度,在B处望占塔的顶部,仰角是60°,在A处再次望古塔的顶部,仰角为45°.
如图,已知瞭望塔BA的高度为40m,为测得古塔DC的高度,在B处望占塔的顶部,仰角是60°,在A处再次望古塔的顶部,仰角为45°.