题目内容
19.设O为△ABC的外心,且$\overrightarrow{OA}+\overrightarrow{OB}+\sqrt{3}\overrightarrow{OC}=\overrightarrow 0$,则△ABC的内角C=( )| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
分析 设△ABC的外接圆的半径为R,由$\overrightarrow{OA}+\overrightarrow{OB}+\sqrt{3}\overrightarrow{OC}=\overrightarrow 0$,化为$\overrightarrow{OA}+\overrightarrow{OB}$=-$\sqrt{3}\overrightarrow{OC}$,两边作数量积运算可得:$(\overrightarrow{OA}+\overrightarrow{OB})^{2}$=$3{\overrightarrow{OC}}^{2}$,化简即可得出.
解答 解:设△ABC的外接圆的半径为R,
由$\overrightarrow{OA}+\overrightarrow{OB}+\sqrt{3}\overrightarrow{OC}=\overrightarrow 0$,化为$\overrightarrow{OA}+\overrightarrow{OB}$=-$\sqrt{3}\overrightarrow{OC}$,
两边作数量积运算可得:$(\overrightarrow{OA}+\overrightarrow{OB})^{2}$=$3{\overrightarrow{OC}}^{2}$,
化为2R2+2R2cos∠AOB=3R2,
化为cos∠AOB=$\frac{1}{2}$,∠AOB∈(0,π),
可得∠AOB=$\frac{π}{3}$,
∴∠C=$\frac{1}{2}$∠AOB=$\frac{π}{6}$,
故选:A.
点评 本题考查了向量数量积运算性质、圆心角与圆周角直角的关系,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
9.某几何体的三视图如图所示,则该几何体的体积为( )
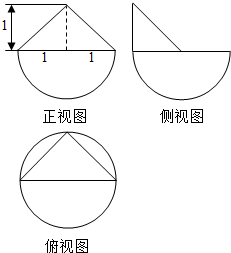

| A. | $\frac{2π+1}{3}$ | B. | $\frac{2π+3}{3}$ | C. | $\frac{4π+1}{3}$ | D. | $\frac{4π+3}{3}$ |
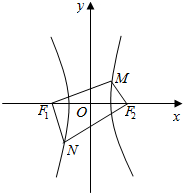 如图,F1,F2是双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点,作过F1作两条相互垂直的直线l1,l2,其中直线l1交双曲线右支于点M,直线l2交双曲线左支于点N,以下说法一定正确的是④
如图,F1,F2是双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点,作过F1作两条相互垂直的直线l1,l2,其中直线l1交双曲线右支于点M,直线l2交双曲线左支于点N,以下说法一定正确的是④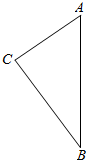 已知等腰三角形ABC中CA=CB,底边长AB=2,现以边AB为轴旋转一周,得旋转体.
已知等腰三角形ABC中CA=CB,底边长AB=2,现以边AB为轴旋转一周,得旋转体. 正方体中,E,F,G分别是A′D′、B′C′、D′C′的中点.
正方体中,E,F,G分别是A′D′、B′C′、D′C′的中点.