题目内容
设f(x)=log
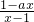 (a为常数)的图象关于原点对称
(a为常数)的图象关于原点对称
(1)求a的值;
(2)判断函数f(x)在区间(1,+∞)的单调性并证明;
(3)若对于区间[3,4]上的每一个x的值,f(x)>( )x+m恒成立,求实数m的取值范围.
)x+m恒成立,求实数m的取值范围.
解:(1)由题意可得,f(x)为奇函数,故有 f(-x)=-f(x),即  =-
=-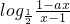 ,
,
即 =
=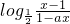 ,∴
,∴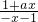 =
=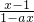 ,解得a=±1. …
,解得a=±1. …
经检验,当a=1时不合条件,故a=-1.
(2)由(1)可得f(x)=log
 ,函数在区间(1,+∞)内单调递增.
,函数在区间(1,+∞)内单调递增.
证明:令g(x)= =1+
=1+ ,由于
,由于 在 区间(1,+∞)内单调递减,
在 区间(1,+∞)内单调递减,
故函数g(x)在区间(1,+∞)内单调递减,故函数f(x)=log
 在区间(1,+∞)内单调递增.
在区间(1,+∞)内单调递增.
(3)令h(x)=f(x)- ,则由(2)得h(x)在[3,4]上单调递增,
,则由(2)得h(x)在[3,4]上单调递增,
故g(x)的最小值为g(3)=- .
.
m<- .
.
分析:(1)由题意可得,f(x)为奇函数,故有 f(-x)=-f(x),即 =-
=-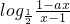 ,化简可得
,化简可得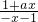 =
=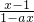 ,由此解得a的值.
,由此解得a的值.
(2)由(1)可得f(x)=log
 ,令 g(x)=
,令 g(x)= =1+
=1+ ,由于
,由于 在 区间(1,+∞)内单调递减,可得函数g(x)在区间(1,+∞)内
在 区间(1,+∞)内单调递减,可得函数g(x)在区间(1,+∞)内
单调递减,从而得到函数f(x)=log
 在区间(1,+∞)内单调递增.
在区间(1,+∞)内单调递增.
(3)令h(x)=f(x)- ,则由(2)得h(x)在[3,4]上单调递增,故g(x)的最小值为g(3),运算求得结果.
,则由(2)得h(x)在[3,4]上单调递增,故g(x)的最小值为g(3),运算求得结果.
点评:本题主要考查函数的奇偶性和单调性,汗水肚饿恒成立问题,求函数的值域,属于中档题.
 =-
=-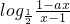 ,
,即
 =
=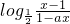 ,∴
,∴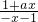 =
=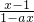 ,解得a=±1. …
,解得a=±1. …经检验,当a=1时不合条件,故a=-1.
(2)由(1)可得f(x)=log

 ,函数在区间(1,+∞)内单调递增.
,函数在区间(1,+∞)内单调递增.证明:令g(x)=
 =1+
=1+ ,由于
,由于 在 区间(1,+∞)内单调递减,
在 区间(1,+∞)内单调递减,故函数g(x)在区间(1,+∞)内单调递减,故函数f(x)=log

 在区间(1,+∞)内单调递增.
在区间(1,+∞)内单调递增.(3)令h(x)=f(x)-
 ,则由(2)得h(x)在[3,4]上单调递增,
,则由(2)得h(x)在[3,4]上单调递增,故g(x)的最小值为g(3)=-
 .
.m<-
 .
.分析:(1)由题意可得,f(x)为奇函数,故有 f(-x)=-f(x),即
 =-
=-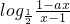 ,化简可得
,化简可得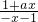 =
=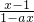 ,由此解得a的值.
,由此解得a的值.(2)由(1)可得f(x)=log

 ,令 g(x)=
,令 g(x)= =1+
=1+ ,由于
,由于 在 区间(1,+∞)内单调递减,可得函数g(x)在区间(1,+∞)内
在 区间(1,+∞)内单调递减,可得函数g(x)在区间(1,+∞)内单调递减,从而得到函数f(x)=log

 在区间(1,+∞)内单调递增.
在区间(1,+∞)内单调递增.(3)令h(x)=f(x)-
 ,则由(2)得h(x)在[3,4]上单调递增,故g(x)的最小值为g(3),运算求得结果.
,则由(2)得h(x)在[3,4]上单调递增,故g(x)的最小值为g(3),运算求得结果.点评:本题主要考查函数的奇偶性和单调性,汗水肚饿恒成立问题,求函数的值域,属于中档题.

练习册系列答案
相关题目
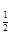 (
(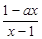 )为奇函数,a为常数.
)为奇函数,a为常数.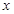 的值,不等式
的值,不等式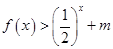 恒成立,求实数
恒成立,求实数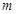 的取值范围.
的取值范围.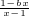 为奇函数,b为常数.
为奇函数,b为常数.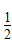
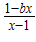 为奇函数,b为常数.
为奇函数,b为常数. )x+m恒成立,求实数m的取值范围.
)x+m恒成立,求实数m的取值范围.