题目内容
10．求证：双曲线x2-15y2=15与椭圆$\frac{{x}^{2}}{25}+\frac{{y}^{2}}{9}$=1的焦点相同．分析 先将双曲线的方程化为标准方程，求出双曲线和椭圆的焦点，即可判断．
解答 证明：双曲线x2-15y2=15即为：
$\frac{{x}^{2}}{15}$-y2=1，c2=a2+b2=15+1=16，c=4，
焦点为（±4，0），
椭圆$\frac{{x}^{2}}{25}+\frac{{y}^{2}}{9}$=1的a′=5，b′=3，c′=4，
焦点为（±4，0），
即有双曲线x2-15y2=15与椭圆$\frac{{x}^{2}}{25}+\frac{{y}^{2}}{9}$=1的焦点相同．
点评 本题考查椭圆和双曲线的方程和性质，注意它们的区别，考查运算能力，属于基础题．
练习册系列答案
相关题目
18．已知定义在R上奇函数f（x）满足f（1+x）=f（1-x）且f（x）在区间[3，5]上单调递增，则函数f（x）在区间[1，3]上的（ ）
| A． | 最大值是f（1），最小值是f（3） | B． | 最大值是f（3），最小值是f（1） | ||
| C． | 最大值是f（1），最小值是f（2） | D． | 最大值是f（2），最小值是f（3） |
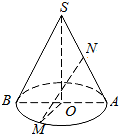已知圆锥的底面半径r=2，半径OM与母线SA垂直，N是SA中点，NM与高SO所成的角为α，tanα=2．则圆锥的体积为$\frac{4\sqrt{5}}{3}π$．
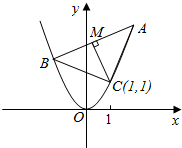过抛物线y=x2上定点C（1，1）引两条互相垂直的弦CA、CB，作CM⊥AB，M为垂足，求点M的轨迹方程．