题目内容
5.在平面直角坐标系xOy中,已知两点E(-1,0)和F(1,0),动点M满足$\overrightarrow{EM}•\overrightarrow{FM}$=0,设点M的轨迹为C,半抛物线C′:y2=2x(y≥0),设点$D(\frac{1}{2}\;,\;0)$.(Ⅰ)求C的轨迹方程;
(Ⅱ)设点T是曲线C′上一点,曲线C′在点T处的切线与曲线C相交于点A和点B,求△ABD的面积的最大值及点T的坐标.
分析 (Ⅰ)由$\overrightarrow{EM}•\overrightarrow{FM}$=0,得(x+1)(x-1)+y2=1,即可求C的轨迹方程;
(Ⅱ)求出曲线C′在点T处的切线与曲线C联立,过点D作x轴的垂线交直线AB于点R,即可求△ABD的面积的最大值及点T的坐标.
解答 解:(Ⅰ)设点M(x,y),由$\overrightarrow{EM}•\overrightarrow{FM}$=0,得(x+1)(x-1)+y2=1,
所以C的轨迹方程是x2+y2=1;
(Ⅱ)抛物线C′为y=$\sqrt{2}{x}^{\frac{1}{2}}$,设T($\frac{1}{2}$t2,t)(t>0),则y′=$\frac{1}{\sqrt{2x}}$,
所以切线为:y-t=$\frac{1}{t}$(x-$\frac{1}{2}$t2)
即2x-2ty+t2=0,联立x2+y2=1,可得4(1+t2)x2+4t2x+t4-4t2=0,
判别式△=16t2(-t4+4t2+4),
设A(x1,y1),B(x2,y2),则|x1-x2|=$\frac{t\sqrt{-{t}^{4}+4{t}^{2}+4}}{1+{t}^{2}}$
过点D作x轴的垂线交直线AB于点R,于是得R($\frac{1}{2}$,$\frac{{t}^{2}-1}{2t}$),则|DR|=$\frac{{t}^{2}+1}{2t}$,
故△ABD的面积S=$\frac{1}{2}$×|DR||x1-x2|=$\frac{\sqrt{-({t}^{2}-2)^{2}-8}}{4}$≤$\frac{{\sqrt{2}}}{2}$,此时$T(1\;,\;\sqrt{2})$.
点评 本题考查轨迹方程,考查直线与圆的位置关系,考查三角形面积的计算,考查学生分析解决问题的能力,属于中档题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | (1,0) | B. | (0,-1) | C. | (1,1) | D. | (1,-1) |
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\sqrt{e}$ | D. | e |
| A. | -1<m<3 | B. | -3<m<-1 | C. | 1<m<3 | D. | 2<m<3 |
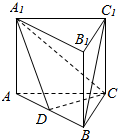 如图,在三棱柱A1B1C1中,四边形ABB1A1和ACC1A1都为矩形.
如图,在三棱柱A1B1C1中,四边形ABB1A1和ACC1A1都为矩形.