Question

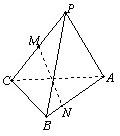
如图，P△ABC所在平面外一点，PA=PB，CB⊥平面PAB，M是PC中点，N是AB上的点，AN=3NB，
（1）求证：MN⊥AB；
（2）当∠PAB=90°，BC=2，AB=4时，求MN的长．

Answer 1

（1）证明：取AB中点Q，连接PQ，CQ，
因为CB⊥平面PAB，则PQ⊥BC，又PA=PB，所以PQ⊥AB，
于是PQ⊥平面ABC，所以∠PQC=90°，
因为M是PC中点，所以MQ=

1

2

PC，
又因为∠CBP=90°，所以MB=

1

2

PC，所以MB=MQ；
而N是BQ的中点，所以MN⊥AB；
（2）当∠PAB=90°，BC=2，AB=4时，
有PB=2

2

，PC=2

3

，MB=

1

2

PC=

3

，
所以MN=

MB2-BN2

=

2

．