题目内容
7.在平面直角坐标xOy中,已知曲线C的参数方程为$\left\{\begin{array}{l}x=\frac{1}{2}{t^2}\\ y=\frac{1}{4}t\end{array}$(t为参数),曲线与直线l:y=$\frac{1}{2}$x相交于A,B两点,求线段AB的长.分析 将曲线C的参数方程化为普通方程为:x=8y2(亦可直接用参数方程解A,B点),与直线l构造方程组$\left\{\begin{array}{l}x=8{y^2}\\ x=2y\end{array}\right.$,解得求出点的坐标,根据点到点的距离公式即可求出答案.
解答 解:∵$\left\{\begin{array}{l}x=\frac{1}{2}{t^2}\\ y=\frac{1}{4}t\end{array}$,
∴x=$\frac{1}{2}$(4y)2,
即x=8y2,
∴方程组$\left\{\begin{array}{l}x=8{y^2}\\ x=2y\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=0}\\{y=0}\end{array}\right.$或$\left\{\begin{array}{l}{x=\frac{1}{2}}\\{y=\frac{1}{4}}\end{array}\right.$,
所以$A(0,0),B(\frac{1}{2},\frac{1}{4})$,
故AB=$\sqrt{(\frac{1}{2}-0)^{2}+(\frac{1}{4}-0)^{2}}$=$\frac{\sqrt{5}}{4}$.
点评 本题主要考查了直线与抛物线的位置关系:相交关系的应用,考查学生的计算能力,属于基础题.

练习册系列答案
相关题目
18.已知x,y满足约束条件$\left\{{\begin{array}{l}{0≤x≤2}\\{x+y-2≥0}\\{kx-y+2≥0(k>0)}\end{array}}\right.$,若目标函数z=x+2y的最大值为10,则k的值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | 1 | D. | 2 |
2.已知f(x)=$\sqrt{3}$sinx-cosx,f′(x)是f(x)的导函数,若f(x0)=$\frac{1}{2}$,则f′(2x0-$\frac{π}{6}$)=( )
| A. | -$\frac{7}{8}$ | B. | $\frac{7}{8}$ | C. | -$\frac{7}{4}$ | D. | $\frac{7}{4}$ |
12.下列命题中,真命题是( )
| A. | ?x0∈R,ex<0 | |
| B. | 若a,b∈R,a+b=0的充要条件是$\frac{a}{b}$=-1 | |
| C. | 命题p:?x∈R,f(x)≥0,则?p:?x0∈R,f(x)<0 | |
| D. | 命题“在△ABC中,若$\overrightarrow{AB}•\overrightarrow{BC}$<0,则△ABC为钝角三角形的逆命题为真命题 |
19.若实数x,y满足$\left\{\begin{array}{l}{x-y+1≥0}\\{x+y≥0}\\{x≤0}\end{array}\right.$,则z=x+2y+a的最小值是2,则实数a的值为( )
| A. | O | B. | $\frac{3}{2}$ | C. | 2 | D. | -l |
17.等差数列{an}的前n项和为Sn,若a2+a7+a12=15,则S13的值是( )
| A. | 45 | B. | 65 | C. | 80 | D. | 130 |
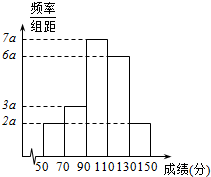 贵阳市某数学教师从他所教的2015届高三(X)班与高三(Y)班学生的高考数学成绩中,随机抽取20名学生的成绩绘制成频率分布直方图,如图所示.
贵阳市某数学教师从他所教的2015届高三(X)班与高三(Y)班学生的高考数学成绩中,随机抽取20名学生的成绩绘制成频率分布直方图,如图所示.