题目内容
（2013•枣庄一模）已知函数f（x）=x2+1的定义域为[a，b]（a＜b），值域为[1，5]，则在平面直角坐标系内，点（a，b）的运动轨迹与两坐标轴围成的图形的面积为（ ）
分析：对于函数f（x）=x2+1而言，当x=±2时，y=5，从而结合题意得出a，b的取值范围．点（a，b）的运动轨迹是两条线段，与两坐标轴围成的图形是一个边长为2的正方形，从而得出结果．
解答：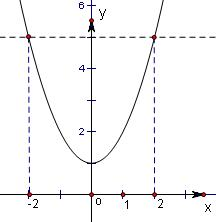
解：对于函数f（x）=x2+1，当x=±2时，y=5．
故根据题意得a，b的取值范围为：-2≤a≤0且b=2或a=-2且0≤b≤2．
∴点（a，b）的运动轨迹与两坐标轴围成的图形是一个边长为2的正方形
面积为4．
故选C．
解：对于函数f（x）=x2+1，当x=±2时，y=5．故根据题意得a，b的取值范围为：-2≤a≤0且b=2或a=-2且0≤b≤2．
∴点（a，b）的运动轨迹与两坐标轴围成的图形是一个边长为2的正方形
面积为4．
故选C．
点评：本小题主要考查二次函数的图象、二次函数的性质、轨迹等基础知识，考查运算求解能力，考查数形结合思想．属于基础题．
练习册系列答案
智慧小复习系列答案
相关题目