Question

【题目】选修4-4：坐标系与参数方程

已知曲线的极坐标方程是,以极点为平面直角坐标系的原点，极轴为轴的正半轴, 建立平面直角坐标系，在平面直角坐标系中, 直线经过点,倾斜角．

（1）写出曲线直角坐标方程和直线的参数方程；

（2）设与曲线相交于两点, 求的值．

Answer 1

【答案】（1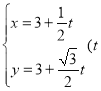），为参数）；（2）．

【解析】

试题分析：（1）曲线化为:,利用可得直角坐标方程，直线经过点,倾斜角可得直线的参数方程；（2）将的参数方程代入曲线的直角坐标方程，利用韦达定理及直线参数方程的几何意义可求得的值．

试题解析：（1）曲线化为:, 再化为直角坐标方程为

,化为标准方程是,直线的参数方程为

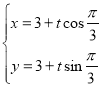,即 为参数）．

（2）将的参数方程代入曲线的直角坐标方程,得 ,整理得:,

,则,所以．