��Ŀ����
ij����̨��A��B��������������Ϸ���ס��ҡ����������˲μӣ����м������˸��Զ���������ϷA���������˸��Զ���������ϷB.��֪�ס������˸��Դ��سɹ��ĸ��ʾ�Ϊ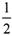 �����������˸��Դ��سɹ��ĸ��ʾ�Ϊ
�����������˸��Դ��سɹ��ĸ��ʾ�Ϊ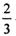 .
.
(I )����ϷA�����سɹ�������������ϷB�����سɹ��������ĸ��ʣ�
(II) ����ϷA��B�����سɹ���������Ϊ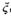 ����
����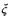 �ķֲ��к�����.
�ķֲ��к�����.
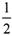 �����������˸��Դ��سɹ��ĸ��ʾ�Ϊ
�����������˸��Դ��سɹ��ĸ��ʾ�Ϊ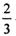 .
.(I )����ϷA�����سɹ�������������ϷB�����سɹ��������ĸ��ʣ�
(II) ����ϷA��B�����سɹ���������Ϊ
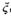 ����
����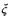 �ķֲ��к�����.
�ķֲ��к�����.��1��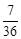 ��2��E
��2��E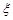 =
=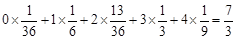
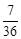 ��2��E
��2��E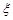 =
=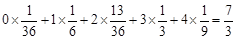
(I )���������ϷA�����سɹ�������������ϷB�����سɹ��������������¼���(II)ȷ��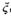 ��ȡֵ���ֱ�����ʣ�д���ֲ��в���������
��ȡֵ���ֱ�����ʣ�д���ֲ��в���������
�⣺��I���衰i������ϷA���سɹ���Ϊ�¼�Ai(i=0��1��2)����j������ϷB���سɹ���Ϊ�¼�Bj(j=0��1��2)��
����ϷA�����سɹ�������������ϷB�����ص�������ΪA1B0+A2B1+A2B0��
�� P(A1B0+A2B1+A2B0)
=P(A1B0)+P(A2B1)+P(A2B0)
=P(A1)��P(B0)+P(A2)��P(B1)+P(A2)��P(B0)
=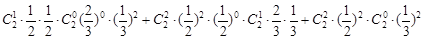
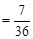 ������ϷA�����سɹ�������������ϷB�����ص������ĸ���Ϊ
������ϷA�����سɹ�������������ϷB�����ص������ĸ���Ϊ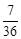 ������4��
������4��
��II���������֪����=0��1��2��3��4��
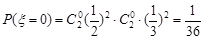 ��
��
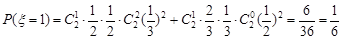 ��
��
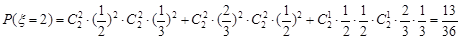 ��
��
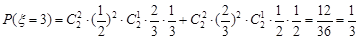 ��
��
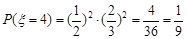 ��
��
��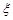 �ķֲ���Ϊ��
�ķֲ���Ϊ��
����������������������������������������������������10��
�� E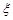 =
=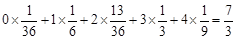 ��
��
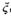 ��ȡֵ���ֱ�����ʣ�д���ֲ��в���������
��ȡֵ���ֱ�����ʣ�д���ֲ��в����������⣺��I���衰i������ϷA���سɹ���Ϊ�¼�Ai(i=0��1��2)����j������ϷB���سɹ���Ϊ�¼�Bj(j=0��1��2)��
����ϷA�����سɹ�������������ϷB�����ص�������ΪA1B0+A2B1+A2B0��
�� P(A1B0+A2B1+A2B0)
=P(A1B0)+P(A2B1)+P(A2B0)
=P(A1)��P(B0)+P(A2)��P(B1)+P(A2)��P(B0)
=
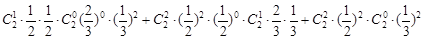
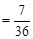 ������ϷA�����سɹ�������������ϷB�����ص������ĸ���Ϊ
������ϷA�����سɹ�������������ϷB�����ص������ĸ���Ϊ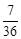 ������4��
������4����II���������֪����=0��1��2��3��4��
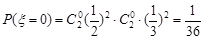 ��
��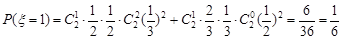 ��
��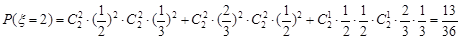 ��
��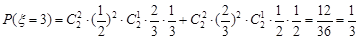 ��
��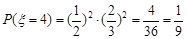 ��
����
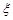 �ķֲ���Ϊ��
�ķֲ���Ϊ��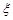 | 0 | 1 | 2 | 3 | 4 |
| P | 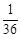 | 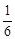 | 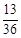 | 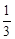 | 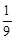 |
�� E
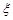 =
=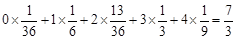 ��
��
��ϰ��ϵ�д�
 ��У����ϵ�д�
��У����ϵ�д�
�����Ŀ
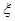 ��������öӲ����2�Σ������泯�ϵĴ���Ϊ
��������öӲ����2�Σ������泯�ϵĴ���Ϊ ��
��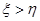 �����ʤ����
�����ʤ����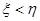 �����һ�ʤ���ֱ�������һ�ʤ�ĸ���.
�����һ�ʤ���ֱ�������һ�ʤ�ĸ���. ����������ʽ�е���
����������ʽ�е���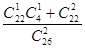 ����( )
����( )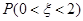
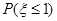
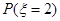

 ��������ȡһ����
��������ȡһ���� �����ٴ�����һ��������
�����ٴ�����һ�������� ����
���� ��ʹ��
��ʹ�� ���ĸ��ʣ�
���ĸ��ʣ� Ϊ��ɸ�������ͬ���ֵĸ��������ֵ����
Ϊ��ɸ�������ͬ���ֵĸ��������ֵ���� ��
��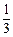 ��ijֲ���о���������С��ֱ������չ�����ӵķ�ѿʵ�飬ÿ��ʵ����һ�����ӣ��ٶ�ij��ʵ�����ӷ�ѿ��Ƹô�ʵ���dzɹ��ģ��������û�з�ѿ����Ƹô�ʵ����ʧ�ܵģ�
��ijֲ���о���������С��ֱ������չ�����ӵķ�ѿʵ�飬ÿ��ʵ����һ�����ӣ��ٶ�ij��ʵ�����ӷ�ѿ��Ƹô�ʵ���dzɹ��ģ��������û�з�ѿ����Ƹô�ʵ����ʧ�ܵģ�