题目内容
若定义在R上的减函数y=f(x),对任意的a,b∈R,不等式f(a2-2a)≤f(b2-2b)成立,则当1≤a≤4时,
的取值范围是( )
| b |
| a |
分析:根据y=f(x)是定义在R上的减函数,得不等式f(a2-2a)≤f(b2-2b)等价于(a-b)(a+b-2)≥0.作出aob直角坐标系如图,画出不等式组
表示的平面区域,将动点P(a,b)在区域内运动并结合直线的斜率公式,可得
的取值范围.
|
| b |
| a |
解答:解:∵函数y=f(x)是定义在R上的减函数,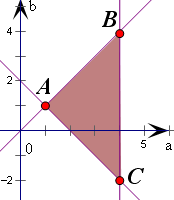
∴任意的a,b∈R,不等式f(a2-2a)≤f(b2-2b)成立,
即a2-2a≥b2-2b,化简得(a-b)(a+b-2)≥0
以a、b分别为横坐标和纵坐标,建立aob直角坐标系,
作出不等式组
表示的平面区域,
如右图所示的△ABC,其中A(1,1),B(4,4),C(4,-2)
动点P(a,b)在区域内运动,得
=k,等于直线PO的斜率
当P与线段AB上某点重合时,
达到最大值,(
)max=1
当P与点C重合时,
达到最小值,(
)min=
=-
由此可得,当1≤a≤4时,
的取值范围是[-
,1]
故选C

∴任意的a,b∈R,不等式f(a2-2a)≤f(b2-2b)成立,
即a2-2a≥b2-2b,化简得(a-b)(a+b-2)≥0
以a、b分别为横坐标和纵坐标,建立aob直角坐标系,
作出不等式组
|
如右图所示的△ABC,其中A(1,1),B(4,4),C(4,-2)
动点P(a,b)在区域内运动,得
| b |
| a |
当P与线段AB上某点重合时,
| b |
| a |
| b |
| a |
当P与点C重合时,
| b |
| a |
| b |
| a |
| -2 |
| 4 |
| 1 |
| 2 |
由此可得,当1≤a≤4时,
| b |
| a |
| 1 |
| 2 |
故选C
点评:本题以函数的单调性为载体,求解不等式恒成立时参数的取值范围,着重考查了函数单调性、二元一次不等式表示的平面区域和直线的斜率公式等知识,属于中档题.

练习册系列答案
相关题目
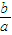 的取值范围是( )
的取值范围是( ) ,1)
,1) ,1]
,1] ,1]
,1] ,1]
,1]