题目内容
若定义在R上的减函数y=f(x),对于任意的x,y∈R,不等式f(x2-2x)≤-f(2y-y2)成立;且函数y=f(x-1)的图象关于点(1,0)对称,则当 1≤x≤4时,
的取值范围
| y |
| x |
[-
,1 ]
| 1 |
| 2 |
[-
,1 ]
.| 1 |
| 2 |
分析:根据函数y=f(x-1)的图象关于点(1,0)对称,可知函数是奇函数,再利用在R上的减函数,转化为具体的不等式,故可解.
解答:解:根据函数y=f(x-1)的图象关于点(1,0)对称,
可知函数是奇函数,
所以由f(x2-2x)≤-f(2y-y2),
得f(x2-2x)≤f(-2y+y2),
∵在R上的减函数y=f(x),
∴x2-2x≥-2y+y2,
,或
,
这两个不等式组表示的平面区域如图所示.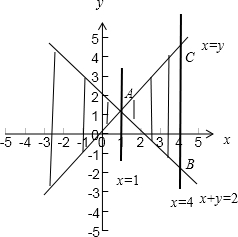
∵1≤x≤4,
∴取两个不等式组表示的平面区域中的△ABC所在的区域,
指的是△ABC区域中的点与原点连线的斜率.
当x=4,y=-2时,
取得最小值-
,
当x=y时,
取得最大值1.
∴-
≤
≤1,
故答案为[-
,1].
可知函数是奇函数,
所以由f(x2-2x)≤-f(2y-y2),
得f(x2-2x)≤f(-2y+y2),
∵在R上的减函数y=f(x),
∴x2-2x≥-2y+y2,
|
|
这两个不等式组表示的平面区域如图所示.

∵1≤x≤4,
∴取两个不等式组表示的平面区域中的△ABC所在的区域,
| y |
| x |
当x=4,y=-2时,
| y |
| x |
| 1 |
| 2 |
当x=y时,
| y |
| x |
∴-
| 1 |
| 2 |
| y |
| x |
故答案为[-
| 1 |
| 2 |
点评:本题主要考查函数的单调性与奇偶性,利用函数为奇函数将不等式等价变形,利用单调性,转化为具体的不等式,要注意细细体会

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
 的取值范围是( )
的取值范围是( ) ,1)
,1) ,1]
,1] ,1]
,1] ,1]
,1]