题目内容
【题目】已知正四棱柱![]() 的底面边长为2,侧棱
的底面边长为2,侧棱![]() 为上底面
为上底面![]() 上的动点,给出下列四个结论:
上的动点,给出下列四个结论:
①若PD=3,则满足条件的P点有且只有一个;
②若![]() ,则点P的轨迹是一段圆弧;
,则点P的轨迹是一段圆弧;
③若PD∥平面![]() ,则DP长的最小值为2;
,则DP长的最小值为2;
④若PD∥平面![]() ,且
,且![]() ,则平面BDP截正四棱柱
,则平面BDP截正四棱柱![]() 的外接球所得图形的面积为
的外接球所得图形的面积为![]() .
.
其中所有正确结论的序号为_____.
【答案】①②④
【解析】
由题意画出图形,求出D与上底面点的最大值判断①;由![]() ,求得PD1为定值判断②;找出满足PD∥平面ACB1的P的轨迹,求出DP长的最小值判断③;由已知求出正四棱住的外接球的半径,进一步求出大圆面积判断④.
,求得PD1为定值判断②;找出满足PD∥平面ACB1的P的轨迹,求出DP长的最小值判断③;由已知求出正四棱住的外接球的半径,进一步求出大圆面积判断④.
如图,

∵正四棱柱ABCD﹣A1B1C1D1的底面边长为2,
∴![]() ,又侧棱AA1=1,
,又侧棱AA1=1,
∴![]() ,则P与B1重合时PD=3,此时P点唯一,故①正确;
,则P与B1重合时PD=3,此时P点唯一,故①正确;
∵![]() ∈(1,3),DD1=1,则
∈(1,3),DD1=1,则![]() ,即点P的轨迹是一段圆弧,故②正确;
,即点P的轨迹是一段圆弧,故②正确;
连接DA1,DC1,可得平面A1DC1∥平面ACB1,则当P为A1C1中点时,DP有最小值为![]() ,故③错误;
,故③错误;
由③知,平面BDP即为平面BDD1B1,平面BDP截正四棱柱ABCD﹣A1B1C1D1的外接球所得平面图形为外接球的大圆,
其半径为![]() ,面积为
,面积为![]() ,故④正确.
,故④正确.
∴正确结论的序号是①②④.
故答案为:①②④.

练习册系列答案
相关题目
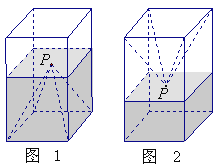
【题目】如图1,一个正四棱柱形的密闭容器底部镶嵌了同底的正四棱锥形实心装饰块,容器内盛有![]() 升水时,水面恰好经过正四棱锥的顶点P.如果将容器倒置,水面也恰好过点
升水时,水面恰好经过正四棱锥的顶点P.如果将容器倒置,水面也恰好过点![]() (图2).有下列四个命题:
(图2).有下列四个命题:
A.正四棱锥的高等于正四棱柱高的一半 |
B.将容器侧面水平放置时,水面也恰好过点 |
C.任意摆放该容器,当水面静止时,水面都恰好经过点 |
D.若往容器内再注入 |
其中真命题的代号是: (写出所有真命题的代号).